Question
Question: As shown in the figure, one block of \( 2.0kg \) at one end and the other of \( 3.0kg \) at the othe...
As shown in the figure, one block of 2.0kg at one end and the other of 3.0kg at the other end of a light string are connected. If this system remains stationary, find the magnitude and direction of the frictional force.
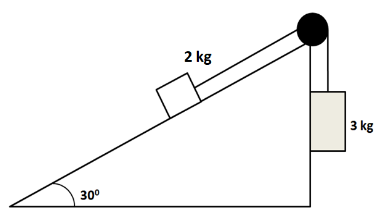
(A) 20N , downward on slope
(B) 20N , upward on slope
(C) 10N , downward on slope
(D) 10N , upward on slope
Solution
To solve this question, we need to apply the conditions of equilibrium on each of the two blocks given in this question to get the equations of translational equilibrium. On solving these equations we will get the final answer.
Complete step-by-step solution
As can be seen in the above figure, a block of 3.0kg is attached to the block of 2.0kg through a string. So it will try to pull the 2.0kg block upward the slope. But the component of weight of the 2.0kg block will try to pull it downward on the slope. Since the 3.0kg block is heavier than the 2.0kg block, so the block will have a tendency to slide upward the slope of the inclined plane. So the friction will act downward on the 2.0kg block. So we can show the different forces acting on the 2.0kg block as shown in the below diagram
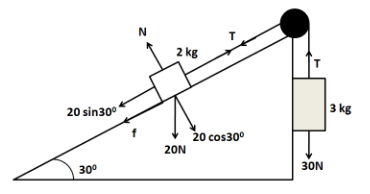
According to the question, the system remains stationary. This means that both the 2.0kg and the 3.0kg blocks must be in equilibrium. Considering the equilibrium of the 3.0kg block, we have
T=30 N .....................(1)
Now, we consider the equilibrium if the 2.0kg block in the direction normal to the incline to get
N=20cos30∘
⇒N=103 N
Similarly considering the equilibrium of the block in the direction parallel to the incline, we have
T=20sin30∘+f
⇒T=10+f
Putting (1) in the above equation, we get
30=10+f
⇒f=20 N
Thus, the frictional force of 20N acts downwards the slope.
Hence, the correct answer is option A.
Note
There was no need to calculate the normal reaction on the 2.0kg block. This is because we were supposed to calculate the frictional force itself, which is easily calculated by the equations of the equilibrium.
