Question

As shown in the figure, forces of ${10^5}$N each are applied in opposite directions, on the upper and lower faces of a cube of side 10cm, shifting the upper face parallel to itself by 0.5cm. If the side of another cube of the same material is 20cm, then under similar conditions as above, the displacement will be:

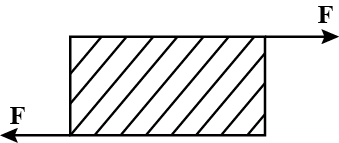
(A) 1.00cm
(B) 0.25cm
(C) 0.37cm
(D) 0.75cm

Answer 1

In order to obtain this solution we should have basic concepts of stress and strain. Here we need to find the stress and strain for both the blocks by considering one by one. After this we can find the displacement.

Complete step by step answer:
According to the diagram, the stress and strain are both the same for the same material.
Let us consider for the 1st block,
Calculating the stress and strain for block 1
Given: F=${10^5}$N
Area=0.1${m^2}$
Change in length=0.5cm
From the formula of stress
$Stress = \dfrac{{Force}}{{Area}}$
$Stress = \dfrac{{{{10}^5}}}{{{{(0.1)}^2}}}$
$\ Strain = \dfrac{{\Delta l}}{l} \\\ Strain = \dfrac{{0.5 \times {{10}^{ - 2}}}}{{0.1}} \\\ \$
Let us consider for the 2nd block,
Calculating the stress and strain for block 2
Here X is the Displacement of the second block.
Given: F=${10^5}$N
Area=0.2${m^2}$
$Stress = \dfrac{{Force}}{{Area}}$
$\ Stress = \dfrac{{{{10}^5}}}{{{{(0.2)}^2}}} \\\ Strain = \dfrac{{\Delta l}}{l} \\\ Strain = \dfrac{X}{{0.2}} \\\ \$

Now let us take ratio of both stress and strain

$$\dfrac{{stres{s_1}}}{{strai{n_1}}} = \dfrac{{stres{s_2}}}{{strai{n_2}}} \\\ \dfrac{{\dfrac{{{{10}^5}}}{{{{0.1}^2}}}}}{{\dfrac{{0.5 \times {{10}^{ - 2}}}}{{0.1}}}} = \dfrac{{\dfrac{{{{10}^5}}}{{{{0.2}^2}}}}}{{\dfrac{X}{{0.2}}}} \\\ \\\$$

X=0.25cm
Hence the correct option is B.

Note: a stress–strain curve for a material gives the relationship between stress and strain. It is obtained by gradually applying load to a test coupon and measuring the deformation, from which the stress and strain can be determined.