Question

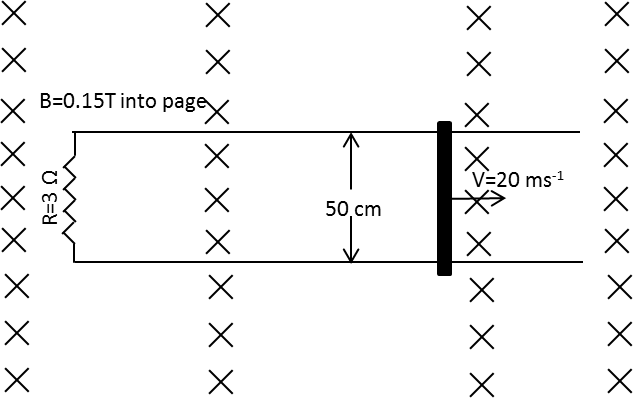
As shown in the figure, a metal rod makes contact with a partial circuit and completes the circuit. The circuit area is perpendicular to a magnetic field with $B = 0.15\,{\text{T}}$. If the resistance out of the total circuit is $3\,\Omega$, the force needed to move the rod as indicated with a constant speed of $2\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$ will be equal to

A. $3.75 \times {10^{ - 3}}$
B. $2.75 \times {10^{ - 3}}$
C. $6.57 \times {10^{ - 4}}$
D. $4.36 \times {10^{ - 4}}$

Answer 1

Use the formulae for the induced emf in the rod, induced current in the rod and the force on the rod moving in the magnetic field. These formulae give the relation between the force on the rod, emf induced, current induced and total resistance.

Formula used:
The emf $e$ induced in the moving rod is
$e = BLv$ …… (1)
Here, $B$ is the magnetic field, $L$ is the length of the moving rod and $v$ is the speed of the moving rod.
The current induced $I$ in a rod moving in the magnetic field is
$I = \dfrac{e}{R}$ …… (2)
Here, $e$ is the emf induced in the rod and $R$ is the resistance.
The force $F$ required to move a rod in the magnetic field is
$F = ILB\sin \theta$ …… (3)
Here, $I$ is the current induced in the rod, $L$ is the length of the rod, $B$ is the magnetic field and $\theta$ is the angle between the current and magnetic field.

Complete step by step answer:
A rod of length $50\,{\text{cm}}$ is moving in the magnetic field of $0.15\,{\text{T}}$ with a speed $2\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$. The total resistance of the circuit is $3\,\Omega$ and the direction of the magnetic field is into the page.

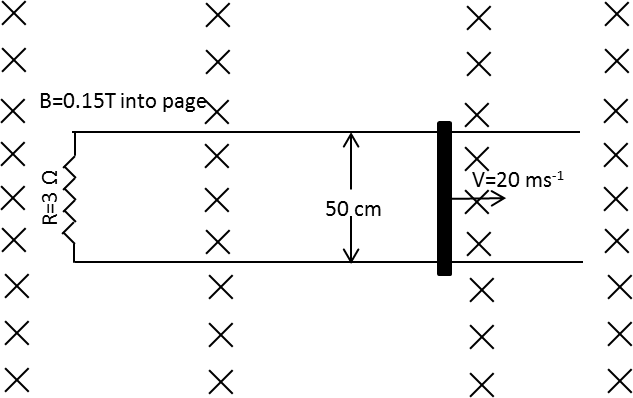
Due to the induced emf, the direction of the induced current in the rod is in the anti-clockwise direction.
Calculate the current induced $I$ in the rod.
Substitute $BLv$ for $e$ in equation (2).
$I = \dfrac{{BLv}}{R}$
Substitute $\dfrac{{BLv}}{R}$ for $I$ in equation (3).
$F = \dfrac{{BLv}}{R}LB\sin \theta$
$\Rightarrow F = \dfrac{{{B^2}{L^2}v\sin \theta }}{R}$
Since the current is in the anti-clockwise direction, the angle between the induced current and the magnetic field is $90^\circ$.
Substitute $0.15\,{\text{T}}$ for $B$, $50\,{\text{cm}}$ for $L$,$2\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$ for $v$, $90^\circ$ for $\theta$ and $3\,\Omega$ for $R$ in equation (1).
$F = \dfrac{{{{\left( {0.15\,{\text{T}}} \right)}^2}{{\left( {50\,{\text{cm}}} \right)}^2}\left( {2\,{\text{m}} \cdot {{\text{s}}^{ - 1}}} \right)\sin 90^\circ }}{{3\,\Omega }}$
$F = \dfrac{{{{\left( {0.15\,{\text{T}}} \right)}^2}{{\left[ {\left( {50\,{\text{cm}}} \right)\left( {\dfrac{{{{10}^{ - 2}}\,{\text{m}}}}{{1\,{\text{cm}}}}} \right)} \right]}^2}\left( {2\,{\text{m}} \cdot {{\text{s}}^{ - 1}}} \right)\sin 90^\circ }}{{3\,\Omega }}$
$\Rightarrow F = 37.5 \times {10^{ - 4}}\,{\text{N}}$
$\Rightarrow F = 3.75 \times {10^{ - 3}}\,{\text{N}}$
Therefore, the force needed to move the rod is $3.75 \times {10^{ - 3}}\,{\text{N}}$.

So, the correct answer is “Option A”.

Note:
According to Fleming’s left hand rule, the rod is required to move the rod in the right direction.
Due to the induced emf, the direction of the induced current in the rod is in the anti-clockwise direction.