Question
Question: As shown in the figure, a long straight conductor with semicircular arc of radius $\frac{\pi}{10} m$...
As shown in the figure, a long straight conductor with semicircular arc of radius 10πm is carrying current I=3A. The magnitude of the magnetic field. at the center O of the arc is: (The permeability of the vacuum = 4π×10−7NA−2)
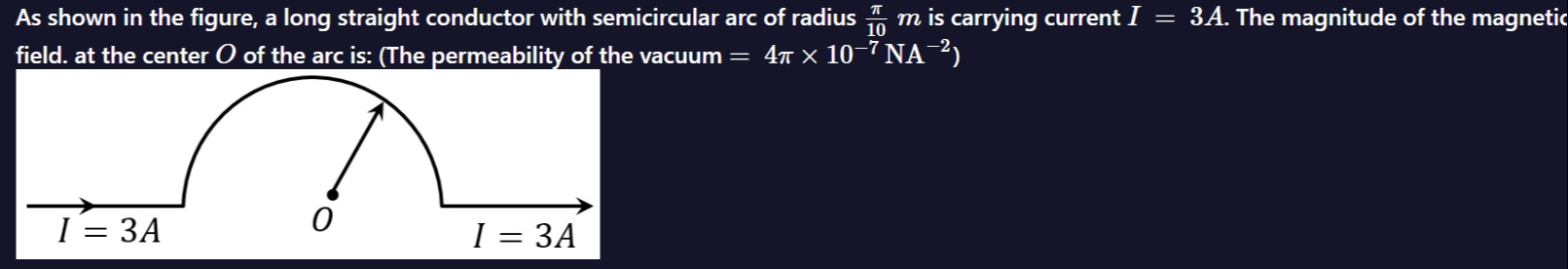
3 × 10−6 T
6 × 10−6 T
9 × 10−6 T
12 × 10−6 T
3 × 10−6 T
Solution
The magnetic field at point O is the sum of the magnetic fields produced by the semicircular arc and the two straight segments.
-
Magnetic field due to the semicircular arc (Barc): The point O is the center of the semicircular arc. The radius of the arc is R=10πm. The angle subtended by a semicircle at its center is θ=π radians. The formula for the magnetic field at the center of a circular arc is B=4πRμ0Iθ. For a semicircle, this becomes: Barc=4πRμ0Iπ=4Rμ0I Given I=3A, R=10πm, and μ0=4π×10−7NA−2: Barc=4×(10πm)(4π×10−7NA−2)×(3A)=4π/1012π×10−7T=4π120π×10−7T=30×10−7T=3×10−6T. The direction of current in the arc is counterclockwise. By the right-hand thumb rule, the magnetic field at O due to the arc is directed out of the page.
-
Magnetic field due to the straight segments (Bstraight): The figure shows that the two straight segments are along the diameter of the semicircle. The point O is the center of the semicircle, and therefore, it lies on the straight segments. The magnetic field at any point lying on a straight current-carrying wire is zero. Thus, Bstraight=0.
-
Total Magnetic Field (Btotal): The total magnetic field at O is the sum of the fields from the arc and the straight segments. Since the straight segments produce zero field at O, the total field is just the field from the arc. Btotal=Barc+Bstraight=3×10−6T+0=3×10−6T.
