Question
Question: As shown in the below figure a variable rheostat of \(2k\Omega \) is used to control the potential d...
As shown in the below figure a variable rheostat of 2kΩ is used to control the potential difference across a 500 ohm load.
(1). If the resistance AB is 500Ω. What is the potential difference across loads?
(2). If the load is removed, what should be the resistance of BC to get 40 Volt between B q C ?
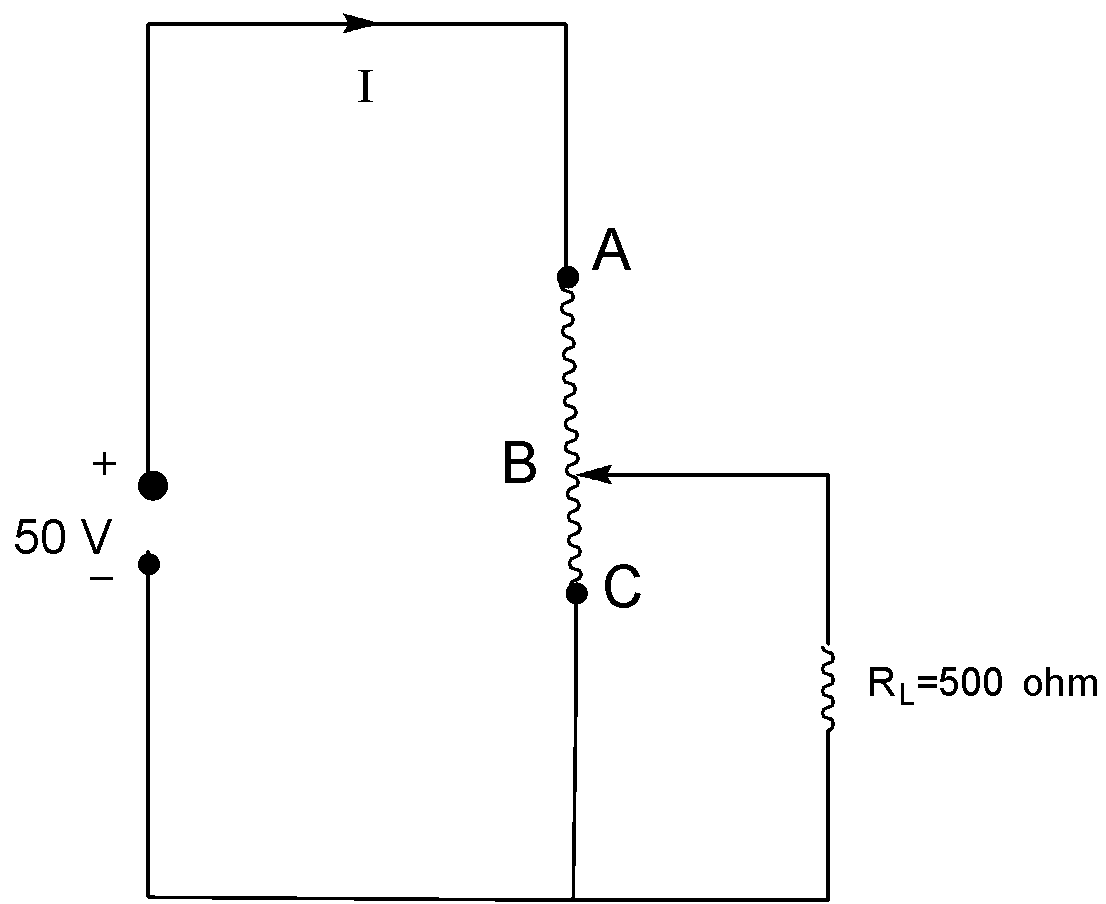
Solution
Resistance: It is the property of any material which obstructs the flow of current.
Resistance in parallel: Two resistors when connected in parallel then the current through each resistor is different and potential difference across (V) Each resistor remains the same. The equivalent resistance of two resistor connected parallel is.
RP1=R11+R21=R1R2R2+R1
Then RP=R1+R2R1R2
Resistances in series: Two or more resistors are said to be connected in series if they are connected end to end and current flows through each resistor is the same.
The equivalent resistance between AB is
RS=R1+R2
Ohm’s Law: According to ohm’s law
V=IR
R=IV
Complete step by step answer:
Step.1 Given
Resistance across AC=RAC=2KΩ=2000Ω
1 kilo ohm = 1000 ohm
Load resistance (RL)=500Ω
Resistance across AB(RAB)=500Ω
Now resistance across BC is.
⟹ RBC=RAC−RAB
Now put the value of RAC and RAB in above given equation
⟹ RBC=2000−500=1500 ohm
Now RBC and RL are in parallel combination.
So total resistance of the parallel combination of RBC and RL is
⟹ R′=1500+5001500×500=2000750000=375Ω
⟹ R′=375
Total resistance of the circuit is.
⟹ R=RAB+R′
⟹ R′ is the resistance of the parallel combination of RAB & RL.
⟹ R=500+375=875
Now the current across the circuit is
By ohm’s law V=IR
I=RV
⟹ I=875Ω50V=352A
⟹ I=352A
1. The potential drop across RL will be the same as the potential drop across R′ ( R′ is the parallel combination of RBC and RL )
Now,
Potential drop across RL is
=V−VAB
⟹ VAB = potential drop across AB
⟹ VAB=352×500
Now we have
=50−352×500=50−28.57=21.43 V
So potential drop across RL=21.43 V
2. If the load is removed then the entire current will flow through resistance RAC of the rheostat.
Now the current across the circuit is.
I′=2000Ω50V=401A
To obtain a potential drop of 40V between B and C, then required resistance BC must be
⟹ RBC′=401A40V=1600Ω
⟹ RBC′=1600Ω
Note:
In series resistance circuit it should be noted.
1. The current through all the resistors is the same.
2. The total resistance of the circuit is equal to the sum of individual resistances including internal resistance of the cell.
3. The potential difference across any resistor is proportional to its resistance.
In a parallel resistance circuit it should be noted.
(1). The total current through parallel combination is equal to the sum of individual currents through the various resistors.
(2). The potential difference across all the resistors is the same.
(3). The current through any resistor is inversely proportional to its resistance.
