Question: As shown in figure, three masses m, 3m, 5m connected together lie on a frictionless horizontal surfa...

Question

As shown in figure, three masses m, 3m, 5m connected together lie on a frictionless horizontal surface and pulled to the left by a force F. The tension ${{T}_{1}}$ in the first string is 24N. (i) find the acceleration of the system (ii) tension in the second string and (iii) force F.

Answer 1

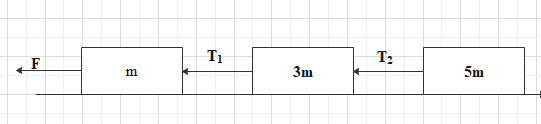
Solution

The acceleration of the system can be written as the force divided by the total mass of the system. Now, the tension on the first string is due to the masses 3m and 5m. putting the expression for acceleration we can find the force on the system. Tension on the second string is due to the mass 5m. Put the given values to find the answer.

Complete step by step answer:
The force on a system can be given by the product of the mass and the acceleration of the system. So, the acceleration of the system can be given by the force divided by the total mass of the system.
Now, the total mass of the system is, $M=m+3m+5m=9m$
The force acting on the system is F.
So, the acceleration of the system is,
$a=\dfrac{F}{M}=\dfrac{F}{9m}$
The tension ${{T}_{1}}$ on the string is given by the
${{T}_{1}}=\left( 3m+5m \right)\times a$
Again, the value of the tension ${{T}_{1}}$ is given as 24N.
Putting the values on the above equation,
$\begin{aligned} & 24N=8m\times \dfrac{F}{9m} \\\ & F=27N \\\ \end{aligned}$
The force on the system is 27N.
So, the acceleration of the system is $a=\dfrac{F}{9m}=\dfrac{27N}{9m}=\dfrac{3}{m}$
Now, the tension ${{T}_{2}}$ on the second string can be given as,
$\begin{aligned} & {{T}_{2}}=5m\times \dfrac{F}{9m} \\\ & {{T}_{2}}=5\times \dfrac{27N}{9} \\\ & {{T}_{2}}=15N \\\ \end{aligned}$
So, the acceleration of the system is $3/m$ , the tension in the second string is 15N and the force on the system is 27N.

Note:
Tension can be defined as the pair of action reaction forces on a rope or string. When we place a weight at one end of the string or rope, we will have a downward force due to the gravity and will have an upward force on the rope or the string which is the tension. The tension is equal to the weight placed at the end.