Question
Question: As shown in figure, a simple harmonic motion oscillator having identical four springs has a time per...
As shown in figure, a simple harmonic motion oscillator having identical four springs has a time period.
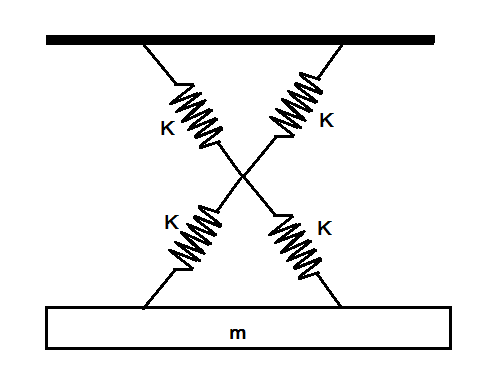
(A) T=2π4Km
(B) T=2π2Km
(C) T=2πKm
(D) T=2π8Km
Solution
Hint : Here, we have been given a figure with four identical spring with equal spring constant and it is given that these are in the simple harmonic motion. These springs are attached to the mass in the end as shown in the figure. We know the formula for the time period of simple harmonic oscillator as:
T=2πKm ; m is mass of the object, K is the spring constant and T is the time period of the simple harmonic oscillator.
Complete Step By Step Answer:
Let us consider the above figure and understand the concept that is to be used in this problem.
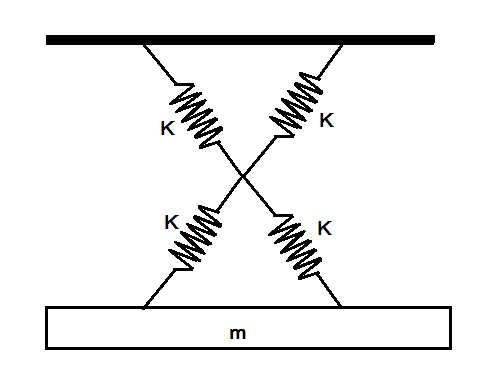
Here, in the above figure we see four springs that are in pairs connected in series and crossed to each other and the mass m is connected at the end of each pair. Each spring is having spring constant K .
Thus, here we have to use the concept of parallel and series combination of the spring constant as we use in resistors in electronic devices. So, the two springs are in parallel with each other, giving an equivalent spring constant as:
K+K=2K …. (1)
Similarly,
The two springs below are also connected in series thus the equivalent is given by:
K+K=2K …. (2)
These two springs are connected in series giving net spring constant for the system as:
2K+2K(2K)(2K)=K …. (From (1) and (2) )
Hence, the time period for simple harmonic oscillator is given by:
T=2πKm
Since, the net spring constant is K .
The correct answer is option C.
Note :
Here, we have calculated the net spring constant by using series and parallel combination of the springs and the mass connected to these springs. We have to understand the concept used here is same as that we use in electronics regarding the resistors combination in series and parallel.
