Question

As observed from the top of a lighthouse, 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from $30{}^\circ \ to\ 40{}^\circ$. Determine the distance travelled by the ship during the period of observation.

Answer 1

Hint:We will be using the concepts of height and distance to solve the problem. We will be drawing the figure according to the situation given and then we will be using trigonometry to further simplify the problem.

Complete step-by-step answer:
Now, we have been given that it is observed from the light house which is 100 m above sea level that the angle of depression of a ship changes from $30{}^\circ \ to\ 40{}^\circ$ and we have to find the distance travelled by ship during this time.
Now, the figure according to the situation is,

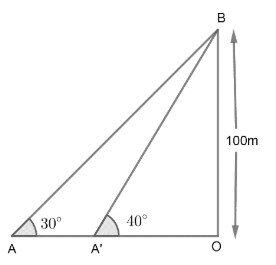
Now, we have to find the distance $AA'$.
So, first we will apply $\tan \theta \ in\ \Delta ABO$. So, we have in $\Delta ABO$,
$\tan \left( 30{}^\circ \right)=\dfrac{P}{B}$
Where P is perpendicular
B is Base.

& \dfrac{1}{\sqrt{3}}=\dfrac{100}{AO} \\\ & AO=100\sqrt{3}m \\\ \end{aligned}$$ Now, in $$\Delta A'BO$$ we have, $\begin{aligned} & \tan \left( 40{}^\circ \right)=\dfrac{BO}{A'O} \\\ & \tan \left( 40{}^\circ \right)=\dfrac{100}{A'O} \\\ & A'O=\dfrac{100}{\tan 40{}^\circ } \\\ \end{aligned}$ Now, the distance travelled by ship during the observation period is, $\begin{aligned} & AO-A'O=AA' \\\ & AA'=\left( 100\sqrt{3}-\dfrac{100}{\tan 40{}^\circ } \right)m \\\ \end{aligned}$ Hence, the distance travelled by ship during observation is $\left( 100\sqrt{3}-\dfrac{100}{\tan 40{}^\circ } \right)m$ Note: To solve these types of questions it is important to know that we have used $\tan \theta $ in both the $\Delta ABO\ and\ \Delta A'BO$ to find the distance travelled by the ship.Students should remember important trigonometric identities ,formulas and important standard angles to solve these types of questions. Also, it is important to know several trigonometric formulae like,$\tan \theta =\dfrac{P}{B},\cos \theta =\dfrac{B}{H},\sin \theta =\dfrac{P}{H}$ where P is Perpendicular from Base,H is Hypotenuse side and B is base.