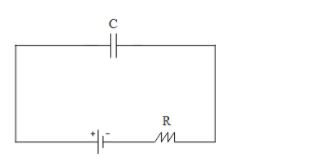
Question

As in the figure shown if a capacitor C is charged by connecting it with resistance R, then energy is given by the battery will be

$\begin{aligned} & a)\dfrac{1}{2}C{{V}^{2}} \\\ & b)\text{More than }\dfrac{1}{2}C{{V}^{2}} \\\ & c)\text{Less than }\dfrac{1}{2}C{{V}^{2}} \\\ & d)Zero \\\ \end{aligned}$

Answer 1

A capacitor connected across a DC supply keeps on charging till the potential across the battery becomes equal to the potential difference across the capacitor. In steady state after some time the current in the circuit will numerically be equal to zero. Hence we will use Kirchhoff law of voltage to see in steady state the potential difference across the capacitor.

Complete step-by-step answer:
The energy stored in a capacitor is given by,
$E=\dfrac{1}{2}C{{V}_{C}}^{2}...(1)$ where C is the capacitance of the capacitor and ${{V}_{C}}$ is the potential difference across the capacitor. When a resistor is connected in series with the capacitor, the voltage across each of them by using Kirchhoff law we get,
$V={{V}_{R}}+{{V}_{C}}..(2)$ where V is the emf of the battery, ${{V}_{C}}$ is the potential difference across the capacitor and ${{V}_{R}}$ is the potential difference across the resistor. In steady state, the current through the circuit becomes zero, hence ${{V}_{R}}=IR=0\text{ since the current in the circuit I is zero}\text{.}$

Therefore, equation 2 can be written as,
$\begin{aligned} & V={{V}_{R}}+{{V}_{C}}\text{ since}{{\text{V}}_{\text{R}}}\text{=0,} \\\ & V={{V}_{C}} \\\ \end{aligned}$
Hence the energy stored in the capacitor from equation 1 we get,
$E=\dfrac{1}{2}C{{V}_{C}}^{2}=\dfrac{1}{2}C{{V}^{2}}$

So, the correct answer is “Option A”.

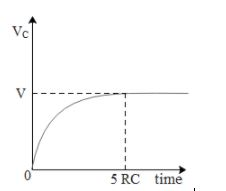
Note: Experimentally the time taken for a capacitor to get completely charged is equal to $5\tau =5RC$ where $\tau$ is the time constant in charging of the capacitor in C-R circuit, R is the resistance of the resistor in series and C is the capacitance of the capacitor. From this we can conclude that adding a resistance in series will increase the time taken by the capacitor to get fully charged. Given below is the graph that shows the charging of a capacitor with time.