Question

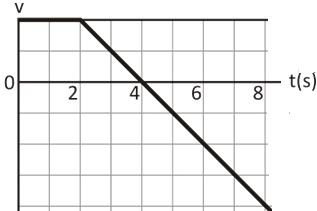
As a runaway scientific balloon ascends at $19.6\,{\text{m}}{{\text{s}}^{ - 1}}$ , one of its packages breaks free of a harness and free-falls. The figure gives the vertical velocity of the package versus time, from before it breaks free to when it reaches the ground. How high is the break-free point above the ground?

Answer 1

First of all, we will find the distance travelled by the balloon above the breakaway point. After that we will find the maximum height reached by the balloon. Lastly, we will subtract the distances found to find the required height of the breakaway point.

Complete step by step answer:
In the given question, we are supplied with the following data:
The runaway scientific balloon moves up with a velocity of $19.6\,{\text{m}}{{\text{s}}^{ - 1}}$ .
One of its packages breaks free of a harness and free-falls.
We are asked to find the height of the break-free point above the ground.

To begin with, we will study the graph provided to us and try to find out the time after which the package breaks free and falls.

For the graph, it can be said that the package breaks free at time equals $2$ seconds because this is the point at which the package starts slowing down and stops ascending at time equals $4$ seconds and its velocity becomes zero, which means it rises only for time equals $2$ seconds.

Now, we have to find the distance it has travelled, we apply one of the equations from the laws of motion:
$s = ut + \dfrac{1}{2}g{t^2}$ …… (1)
Where,
$s$ indicates the distance it has travelled above the breakaway point.
$u$ indicates the initial velocity of the balloon.
$t$ indicates time duration.
$g$ indicates acceleration due to gravity.

Now, we substitute the required values in the equation (1) and we get:
s = ut + \dfrac{1}{2}g{t^2} \\\
\Rightarrow s = 19.6 \times 2 + \dfrac{1}{2} \times \left( { - 9.8} \right) \times {2^2} \\\ \Rightarrow s = 39.2 - 19.6 \\\ \Rightarrow s = 19.6\,{\text{m}} \\\
Therefore, the package rises for a distance of $19.6\,{\text{m}}$ above the breakaway point.

Now, we will calculate the maximum distance up to which the package rises.
From the graph it is clear that the package at the highest point at time equals $4$ seconds. After that time, it falls freely under the influence of gravity. When a body free falls, its initial velocity is zero.
So, by one of the equations of laws of motion, we have:
$s' = ut + \dfrac{1}{2}g{t^2}$ …… (2)
Where,
$s'$ indicates the maximum height the balloon reaches.

Now, we substitute the required values in the equation (2) and we get:
s' = ut + \dfrac{1}{2}g{t^2} \\\ \Rightarrow s' = 0 + \dfrac{1}{2} \times 9.8 \times {4^2} \\\ \Rightarrow s' = 78.4\,{\text{m}} \\\
Therefore, the maximum height is found out to be $78.4\,{\text{m}}$ .

So, the breakaway point is located at:
$\Delta s = s - s'$ …… (3)
Where,
$\Delta s$ is the distance of the breakaway point from the ground.

Now, we substitute the required values in the equation (3) and we get:
\Delta s = s - s' \\\ \Rightarrow \Delta s = 78.4 - 19.6 \\\ \Rightarrow \Delta s = 58.8\,{\text{m}} \\\
Hence, the breakaway point is located at a distance of $58.8\,{\text{m}}$ from the ground.

So, the correct answer is “Option A”.

Note:
It is important to remember that you will need to subtract the distance after the breakaway point to get the distance of the height of the breakaway point above the ground. Always remember that whenever a body free falls, its initial velocity remains zero. One of its packages breaks free of a harness and free-falls.