Question
Question: As a physicist, you put heat into a \(500g\) solid sample at the rate of \(10.0kJ{\min ^{ - 1}}\), w...
As a physicist, you put heat into a 500g solid sample at the rate of 10.0kJmin−1, while recording its temperature as a function of time. You plot your data and obtain the graph as shown in the figure. What is the specific heat of the solid state of the material.
(A). 2.66kJkg−1∘C−1
(B). 4.99kJkg−1∘C−1
(C). 1.33kJkg−1∘C−1
(D). None of these
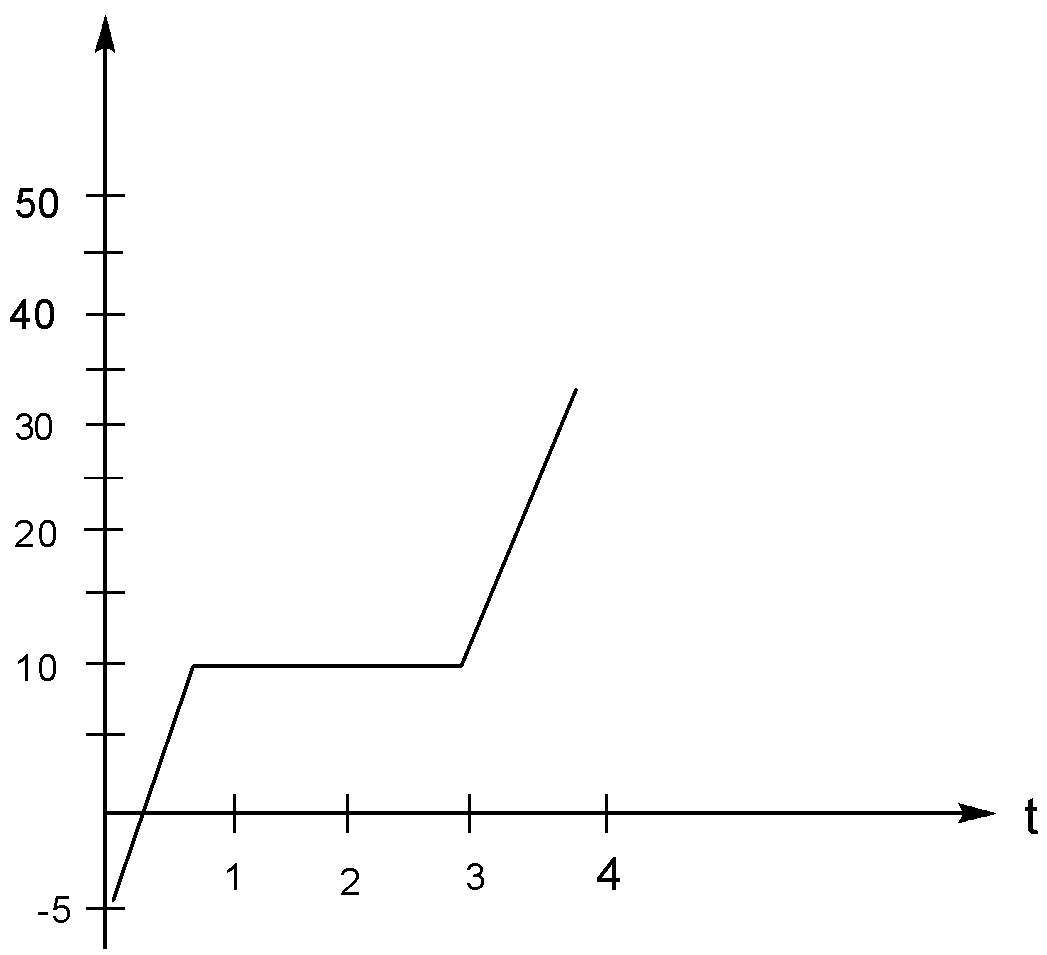
Solution
We know that a solid changes into a liquid at a temperature equal to melting point of the solid. Similarly a liquid changes into a gaseous state at a temperature equals to boiling point of liquid. Temperature remains unaffected as the state of the entire substance has changed. Thus a thermometer fails to detect the change of state as there is neither rise nor fall in temperature duriv the change of state. That is why heat energy spent in change of state is called Latent Heat.
L=mQ
Here, L is the latent heat, Q is the heat absorbed and m is the mass of the body.
Latent heat is measured in Jkg−1 or Calg−1. For example Latent heat of Fusion of ice =80 Calg−1=3.33×10JJkg−1
Complete step by step answer:
Now from the graph it is clear that within the time period,Time (t)=1min to Time (t)=3min
There is no change/rise in the temperature of the substance. Therefore the solid melts in this time period.
Now the Latent heat we have is
⟹ L=mQ=mHT - - - - - - - (1)
Here H is rate of change of heat
T is the time period for heat change.
So now here we have from the question
H=10.0kJmin−1
And T=2
m=0.5
Now putting all the above values in the equation (1) so we have.
⟹ L=0.510×2=40kJkg−1
And also we have the formula for specific heat is
⟹ ΔQ=ms(ΔT)
Here ΔQ is the small amount of heat energy required to raise the temperature of certain mass (m) of a substance through a small range of temperature (ΔT).
Here ′S′ in the formula is called a Constant of proportionality and is called specific heat capacity or simply specific heat of the material of the substance. Q=mSΔT
So now S=m×ΔTQ
Now S=0.5×1510×1=1.33kJkg−1∘C−1
Hence option ‘C’ is correct.
Note: Molar specific heat or molar heat capacity:
It is defined as the amount of heat required to raise the temperature of one gram mole of the substance through a unit degree.
It is represented by ‘C’ .
Now by the definition.
One mole of any substance is Quantity of substance whose mass in gram is numerically equals to the molecular mass (M)
C=Ms
To calculate the no of moles in a given (mgm) of the substance, we divide ′m′ buy the molecular mass (M)
n=Mm or m=nM
Now from the definition of specific heat
S=mΔTΔQ=nM(ΔT)ΔQ
MS=n1(ΔTΔQ)
C=n1(ΔTΔQ)
The above is the expression for the molar specific heat of the substance.
