Solveeit Logo
Login

Question

Question: Arrangement of two block systems is as shown. The net force acting on \(1\,kg\) and \(2\,kg\) blocks...

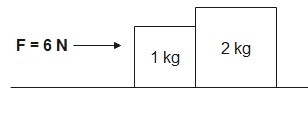
Arrangement of two block systems is as shown. The net force acting on 1 kg1\,kg and 2 kg2\,kg blocks are (assuming the surfaces to be frictionless) respectively
(A). 4 N, 8 N4\,N,\,8\,N
(B). 1 N, 2 N1\,N,\,2\,N
(C). 2 N, 4 N2\,N,\,4\,N
(D). 3 N, 6 N3\,N,\,6\,N

Explanation

Solution

The force of 6 N6\,N acting on the body pushes the other block with some force due to the normal reaction acting between them. By the second law of motion, the force changes the state of rest or motion of an object, so the system starts moving with some acceleration.

Formulas Used:
F=maF=ma

Complete step-by step solution:
Normal force acts between two surfaces in contact. It is also called contact force. A surface exerts a normal force on another surface to prevent the other from passing through it.
Let us consider all the forces acting on the first block

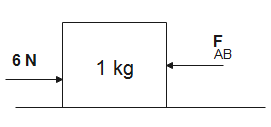
FAB{{F}_{AB}} is the normal force acting on first block due to second block
Therefore,
6−FAB=ma6-{{F}_{AB}}=ma
6−FAB=1×a6-{{F}_{AB}}=1\times a - (1)
Forces acting on the second block will be-

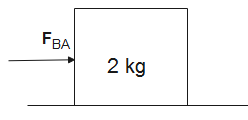
FBA{{F}_{BA}} is the normal force of 1st block on the second block,
Therefore,
FAB=m′a{{F}_{AB}}=m'a
FAB=2×a{{F}_{AB}}=2\times a - (2)
Substituting eq (1) in eq (2), we get,
6−2a=a ⇒6=3a ∴a=3ms−2 \begin{aligned} & 6-2a=a \\\ & \Rightarrow 6=3a \\\ & \therefore a=3m{{s}^{-2}} \\\ \end{aligned}
Both blocks are accelerating with 3ms−23m{{s}^{-2}}
So the force acting on the first block is-
F=ma ⇒F=1×2=2N \begin{aligned} & F=ma \\\ & \Rightarrow F=1\times 2=2N \\\ \end{aligned}
Force acting on the second block is-
F′=m′a ⇒F′=2×2=4N \begin{aligned} & F'=m'a \\\ & \Rightarrow F'=2\times 2=4N \\\ \end{aligned}
Forces acting on both blocks are 2N and 4N2N\,and\,4N respectively.

So, the correct option is (C).

Additional Information:
When a system is isolated, it follows the law of conservation momentum, which states that the total initial momentum of the system is equal to the total final momentum. When a force does no force on the system, then mechanical energy of the system is conserved.

Note:
Normal force is always perpendicular to the surfaces. According to Newton’s third law, the normal forces acting on both surfaces are equal and opposite. The forces acting on each body is directly proportional to their masses. In the two-block system, the contact forces are internal forces while the 6N6N force is an external force acting on the system.