Question

Armaan goes 10 km distance with an average speed of 6 km/hr while the rest 20 km he travels with an average speed of 15 km/hr. What is the average speed of Armaan during the whole journey?

Answer 1

The average speed of an object is calculated by dividing the total distance traveled by the object by the total time taken to complete the journey.

Complete step by step answer:
Armaan travels 10 km with an average speed of 6 km/hr. Then the time taken by Armaan to travel 10 km is
${{T}_{1}}=\dfrac{10\,km}{6\,km/hr}$

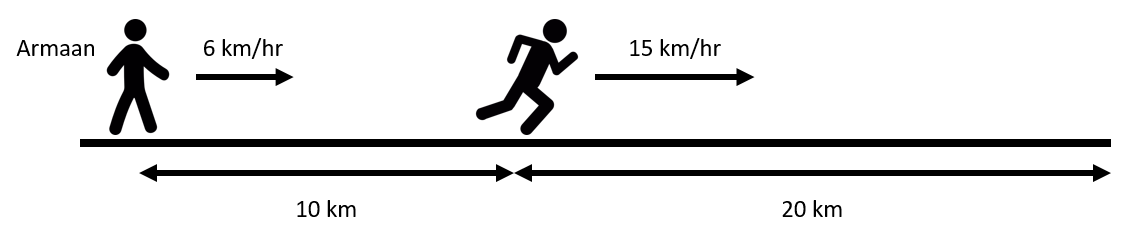
For the next 20 km, Armaan travels with an average speed of 15 km/hr. Therefore, the time taken to cover the second half of the journey is
${{T}_{2}}=\dfrac{20\,km}{15\,km/hr}$
Therefore, the total time taken by Armaan to complete the whole journey will be
$\begin{aligned} & T={{T}_{1}}+{{T}_{2}} \\\ & T=\left( \dfrac{10}{6}+\dfrac{20}{15} \right)\,hr \\\ & T=3\,hr \\\ \end{aligned}$
We know that average speed is equal to the total distance traveled divided by the total time taken to complete the journey. Here, the total distance travel by Armaan is 30 km, therefore the average speed will be
$\begin{aligned} & \text{Avg}\text{. Speed}=\dfrac{\text{Total distance travelled}}{\text{Total time taken}} \\\ & =\dfrac{30\,km}{3\,hr} \\\ & \text{Avg}\text{. Speed}=10\,km/hr \end{aligned}$

Therefore, the average speed of Amaan is 10 km/hr.

Additional Information:
If an object travels with multiple speeds for a different amount of time, the average speed will be
$\text{Avg}\text{. Speed}=\dfrac{{{S}_{1}}{{T}_{1}}+{{S}_{2}}{{T}_{2}}+{{S}_{3}}{{T}_{3}}+......}{{{T}_{1}}+{{T}_{2}}+{{T}_{3}}+......}$
If an object travels with different speeds for the same amount of time (i.e. T1=T2=T3=….=Tn), the average speed will be
$\text{Avg}\text{. Speed}=\dfrac{{{S}_{1}}+{{S}_{2}}+{{S}_{3}}+.....\,\text{n times}}{n}$
If an object travels with two different speeds for the same distances (i.e. D1=D2), the average speed will be
$\text{Avg}\text{. Speed}=\dfrac{2{{S}_{1}}{{S}_{2}}}{{{S}_{1}}+{{S}_{2}}}$
If an object travels with three different speeds for the same distance (i.e. D1=D2), the average speed will be
$\text{Avg}\text{. Speed}=\dfrac{3{{S}_{1}}{{S}_{2}}{{S}_{3}}}{{{S}_{1}}{{S}_{2}}+{{S}_{2}}{{S}_{3}}+{{S}_{3}}{{S}_{1}}}$

Note:
This question can be solved quickly by using the formula:
$\text{Avg}\text{. Speed}=\dfrac{{{S}_{1}}{{S}_{2}}({{D}_{1}}+{{D}_{2}})}{{{S}_{2}}{{D}_{1}}+{{S}_{1}}{{D}_{2}}}$
Here, ${{S}_{1}}=6\,km/hr$, ${{S}_{2}}=15\,km/hr$, ${{D}_{1}}=10\,km/hr$, and ${{D}_{2}}=20\,km/hr$. Therefore, by using the above formula, the average speed of Armaan will be

& \Rightarrow \text{Avg}\text{. Speed}=\dfrac{6\times 15(10+20)}{(15\times 10)+(6\times 20)} \\\ & \Rightarrow \text{Avg}\text{. Speed}=\dfrac{2700}{270}\,km/hr \\\ & \Rightarrow \text{Avg}\text{. Speed}=10\,km/hr \\\ \end{aligned}$$