Question

Area under a $v-t$ graph represents a physical quantity which has the unit ?

Answer 1

Velocity is a vector quantity which has magnitude as well as direction while displacement is also a vector quantity which has magnitude and direction while scalar quantities only have magnitude and no direction.

Complete step by step answer:
Area under the v-t graph means the graph is drawn to show the relation between velocity and time.

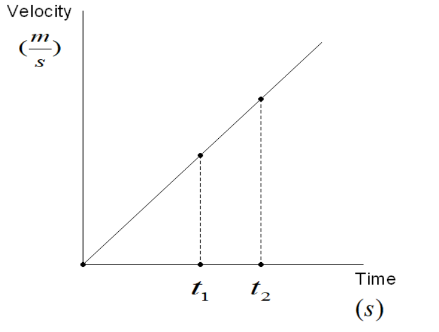
Velocity is the rate of change of displacement that means change in displacement per unit time.
$v=\dfrac{ds}{dt}$
It can be written as:
$ds=vdt$
Take both side integral, we get
$\int{d}s=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{vdt}$
$\Rightarrow s=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{vdt}$
$\Rightarrow s=v({{t}_{2}}-{{t}_{1}})$
Integration of $vdt$ shows area under v-t graph.

From the above analysis we can say the area under the v-t graph shows displacement. We cannot say the area of the v-t graph shows distance because distance is a scalar quantity and velocity is a vector quantity, so the area of the v-t graph has magnitude as well as direction. It means that the area of the v-t graph shows a vector quantity. The S.I unit of velocity is $\dfrac{meter}{\sec ond}(\dfrac{m}{s})$ and the S.I unit of time is $\sec ond(s)$.
Unit of the area under v-t graph is ,
$\text{area under v-t graph }=\text{Velocity}\times \text{Time}$
$\Rightarrow \text{area under v-t graph }=(\dfrac{m}{s})\times (s)$
$\therefore \text{area under v-t graph }=m$

Hence, area under the v-t graph shows displacement and its S.I unit is meters.

Note: We should know units of all physical quantities like in the above question we take units of velocity is $\dfrac{meter}{\sec ond}(\dfrac{m}{s})$. We should know some basic concepts of integration which are used in the above question.