Question

Area of the triangle formed by the pair of tangents drawn from $\left( { - 1,4} \right)$ to ${y^2} = {\text{ }}16x$ and the chord of contact of $\left( { - 1,4} \right)$ is
A) $8\sqrt 2$
B) $16\sqrt 3$
C) $5\sqrt 2$
D) $16\sqrt 2$

Answer 1

Hint : To solve this question, i.e., to find the area of the triangle formed by the pair of tangents drawn from $\left( { - 1,4} \right)$ to ${y^2} = {\text{ }}16x$ and the chord of contact of $\left( { - 1,4} \right),$ we will use the formula of area of triangle formed by the tangents from the point $\left( {x,y} \right)$ to parabola ${y^2} = {\text{ }}4ax\;$ and chord of contact, now on putting the given values in the formula, we will get our required answer.

Complete step-by-step answer :
We need to find the area of the triangle formed by the pair of tangents drawn from $\left( { - 1,4} \right)$ to ${y^2} = {\text{ }}16x$ and the chord of contact of $\left( { - 1,4} \right).$
Let us draw a figure using the above information, to understand better.

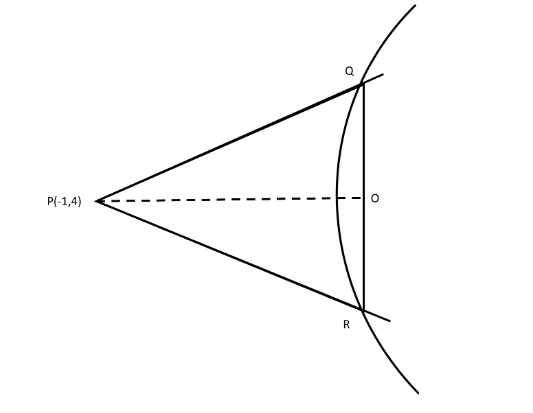
In the above diagram, the chord of contact is P. Q and R are the ends of the chord of contact P.
So, in the question, we have been given the parabola ${y^2} = {\text{ }}16x$ and the points $\left( { - 1,4} \right).$
We know the formula of area of the triangle formed by the tangents from the point $\left( {x,y} \right)$ to parabola ${y^2} = {\text{ }}4ax$ and chord of contact, i.e., Area of the triangle
$= [{\dfrac{{{y_1}^2{\text{ - }}4ax{\;_1}}}{{2a}}]^{\dfrac{3}{2}}}$
On putting the given values, i.e.,
${y_1} = {\text{ }}4,$ $a{\text{ }} = {\text{ }}4$ and ${x_1} = {\text{ }} - 1,$ in the above formula, we get
Area of the triangle $= {\dfrac{{[{{(4)}^2}{\text{ - 16( - 1)]}}}}{{2(4)}}^{\dfrac{3}{2}}}$

$$= {\dfrac{{[16 + {\text{ 16]}}}}{8}^{\dfrac{3}{2}}} \\\ = {4^{\dfrac{3}{2}}} \\\ = 8\sqrt 2 sq.units \\\$$

So, area of the triangle formed by the pair of tangents drawn from $\left( { - 1,4} \right)$ to ${y^2} = {\text{ }}16x$ and the chord of contact of $\left( { - 1,4} \right)$ is $8\sqrt 2$.
So, the correct answer is “Option A”.

Note : In the question, we have been given about tangents and chord of contact, let us understand about them. Tangents are the line which touches the curve with only one point, tangents can be called as tangent lines or only tangents. And chords of contact are the points of contact of two tangents drawn from a point in a circle.