Question

Area of the region bounded by two parabolas $y={{x}^{2}}$ and $x={{y}^{2}}$ is.
(A) $\dfrac{1}{3}$
(B) $3$
(C) $\dfrac{1}{4}$
(D) $4$

Answer 1

For answering this question we will obtain the simplified equation of the bounded region by the two parabolas $y={{x}^{2}}$ and $x={{y}^{2}}$ as follows ${{x}^{2}}-\sqrt{x}$ and integrate it over the intersection points as the limits.

Complete answer:
Now considering from the questions we have two parabolas $y={{x}^{2}}$ and $x={{y}^{2}}$ .These curves can also be written as $y={{x}^{2}}$ and $y=\sqrt{x}$ .
To find the intersection point of both curves we will use ${{x}^{2}}=\sqrt{x}$ which can be simply written as ${{x}^{4}}=x$ .
By further simplifying we will have ${{x}^{4}}-x=0\Rightarrow x\left( {{x}^{3}}-1 \right)=0$ .
Hence, $\left( 0,0 \right)$ and $\left( 1,1 \right)$ are the two points of intersection of the given parabolas.

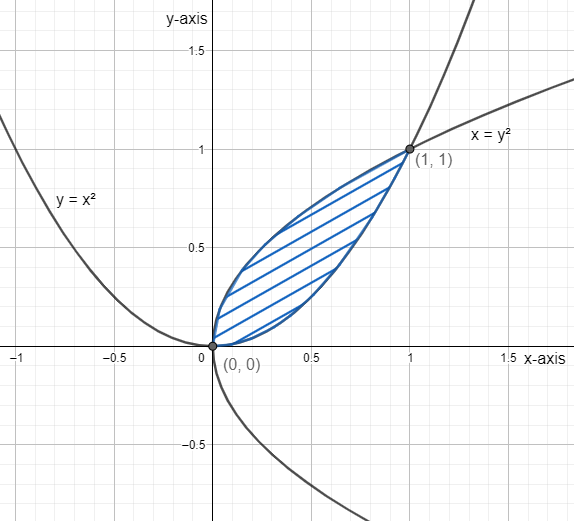
To find the area between the parabolas that is the area under the curve we need to subtract will the upper curve from the lower curve so we will have $\int_{0}^{1}{\left( \sqrt{x}-{{x}^{2}} \right)dx}$ .
As we know that $\int{{{x}^{n}}}dx=\dfrac{{{x}^{n+1}}}{n+1},n\ne -1$ by using this we will have $\int_{0}^{1}{\left( \sqrt{x}-{{x}^{2}} \right)dx}=\left( \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}-\dfrac{{{x}^{3}}}{3} \right)_{0}^{1}$ .
By further simplifying we will have $\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}$ .
Hence, we can conclude that the area of the region bounded by two parabolas $y={{x}^{2}}$ and $x={{y}^{2}}$ is given as $\dfrac{1}{3}$ .

Hence, option A is correct.

Note:
While answering this type of question we should note a point that area can never be negative so we need to apply modulus to the final result. The intersection points should be obtained exactly. This question can be answered in another way by integrating it over the y-limits as follows: $\int_{0}^{1}{\left( {{y}^{2}}-\sqrt{y} \right)dy}=\left( \dfrac{{{y}^{3}}}{3}-\dfrac{{{y}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right)_{0}^{1}=-\dfrac{1}{3}$ the same answer.