Question

Area of the region bounded by the curve $y=\tan x$, tangent drawn to the curve at $x=\dfrac{\pi }{4}$ and the x-axis is:
A. ${}^{1}/{}_{4}$
B. $\log \sqrt{2}+{}^{1}/{}_{4}$
C. $\log \sqrt{2}-{}^{1}/{}_{4}$
D. None of these

Answer 1

Draw the curves of the given equation and get the area bounded by the given curves. Tangent to any curve $y=f(x)$ at point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as $y-{{y}_{1}}=\dfrac{dy}{dx}\int{\begin{matrix} \left( x-{{x}_{1}} \right) \\\ \left( {{x}_{1}},{{y}_{1}} \right) \\\ \end{matrix}}$. Use integration to find the area of the curve with x-axis and the area of the triangle is given as $=\dfrac{1}{2}\times base\times height$.

Complete step by step answer:
As we need to find the area of the region bounded by the curve $y=\tan x$, tangent drawn to the curve at $x=\dfrac{\pi }{4}$, and the x-axis. So we need to draw a neat diagram so that we can visualize the bounded area required in the problem.
Hence, diagram with the help of $y=\tan x$ and tangent to it at $x=\dfrac{\pi }{4}$ can be given as,

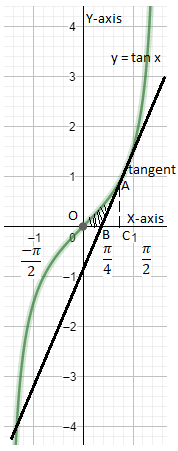
As we can see the shaded region in the above diagram of which we need to find the area.
Now we can observe that the area of the shaded region can be calculated by taking the difference of the area of region OAC and ACB.
So let us calculate the equation of tangent through $x=\dfrac{\pi }{4}$ at $y=\tan x$.
So x coordinate of A is $\dfrac{\pi }{4}$.
Y coordinate can be given by putting $x=\dfrac{\pi }{4}$ to $\begin{aligned} & y=\tan x \\\ & y=\tan \dfrac{\pi }{4}=1 \\\ \end{aligned}$
Hence the coordinate of A is $\left( \dfrac{\pi }{4},1 \right)$.
Now the slope of the tangent can be calculated by finding the derivative of $y=\tan x$ at point 1.
So we got

& y=\tan x \\\ & \dfrac{dy}{dx}=\dfrac{d}{dx}\left( \tan x \right) \\\ \end{aligned}$$ So we know, $$\dfrac{d}{dx}\tan x={{\sec }^{2}}x$$. Hence we get $$\dfrac{d}{dx}={{\sec }^{2}}x....(1)$$ $$\dfrac{dy}{dx}$$ at point A $$\left( \dfrac{\pi }{4},1 \right)$$ is given as, $$\dfrac{dy}{dx}\int{\left( \dfrac{\pi }{4},1 \right)}={{\sec }^{2}}\dfrac{\pi }{4}={{\left( \sqrt{2} \right)}^{2}}=2$$, where we know $$\sec \dfrac{\pi }{4}=\sqrt{2}$$. Hence we can write the equation of tangent with the help of slope and coordinate form which is given as, $$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right).....(2)$$ where $$\left( {{x}_{1}},{{y}_{1}} \right)$$ are the points on line and m is the slope. So equation of tangent. $$\begin{aligned} & y-1=2\left( x-\dfrac{\pi }{4} \right) \\\ & y-1=2x-\dfrac{\pi }{2} \\\ & y=2x+1-\dfrac{\pi }{2}.....(3) \\\ \end{aligned}$$ Now we can calculate the coordinates of point by putting y = 0 to equation (3) as the y-coordinate of point B will always be 0. So we get, $$\begin{aligned} & 0=2x+1-\dfrac{\pi }{2} \\\ & 2x=\dfrac{\pi }{2}-1 \\\ & x=\dfrac{1}{2}\left( \dfrac{\pi }{2}-1 \right) \\\ & x=\dfrac{\pi }{4}-\dfrac{1}{2} \\\ \end{aligned}$$ Hence length BC can be given as, BC = (x-coordinate of C) – (x-coordinate of point B) $$BC=\dfrac{\pi }{4}-\left( \dfrac{\pi }{4}-\dfrac{1}{2} \right)=\dfrac{1}{2}$$ Hence BC = $$\dfrac{1}{2}$$ and AC = 1. So, we know, the area of the triangle is given as the area of triangle $$=\dfrac{1}{2}\times base\times height$$. So, area of $$\Delta ABC$$ $$=\dfrac{1}{2}\times AC\times BC=\dfrac{1}{2}\times 1\times \dfrac{1}{2}=\dfrac{1}{4}uni{{t}^{2}}$$, and area of the region OAC can be calculated by integrating the curve $$y=\tan x$$ from 0 to $$\dfrac{\pi }{4}$$. So, we get the area of OAC $$=\int\limits_{0}^{{}^{\pi }/{}_{4}}{\tan xdx}$$ As we know $$\int{\tan xdx=-\log \cos x+c}$$. So we can get the area of OAC as $$=\int\limits_{0}^{{}^{\pi }/{}_{4}}{\tan xdx}=\int\limits_{0}^{{}^{\pi }/{}_{4}}{-\log \cos x}$$ Area of OAC, $$\begin{aligned} & =-\left( \log \left( \cos \dfrac{\pi }{4} \right)-\log \left( \cos 0 \right) \right) \\\ & =-\left( \log \dfrac{1}{\sqrt{2}}-\log 1 \right) \\\ & =-\left( \log \dfrac{1}{\sqrt{2}}-\log 1 \right) \\\ & =-\left( \log \dfrac{1}{\sqrt{2}}-0 \right) \\\ \end{aligned}$$ Area of OAC $$=-\log \dfrac{1}{\sqrt{2}}$$. As we know, the property of logarithm is that $$\log x=-\log \left( \dfrac{1}{x} \right)$$. So we can get area of OAC as, Area of OAC $$=-\log \sqrt{2}uni{{t}^{2}}$$. Hence area of the shaded region i.e. OAB is given as, Area of OAB = Area of OAC – Area of ABC Area of OAB $$=\log \sqrt{2}-\dfrac{1}{4}$$. **Hence option C is the correct answer.** **Note:** One may calculate the area bounded by the graph with respect to y-axis as well.  Area of OAB = area of OABC – area of OBC So it can be another approach as well. But here, we need to use the area of trapezium (OABC), i.e. given as $$\dfrac{1}{2}$$ (sum of parallel sides) $$\times $$ height. Plotting of the curves given in the problem should be perfect to evaluate the shaded area clearly. And taking care with the calculation part as well as calculation part is also an important side of the question.