Question

Area of the region bounded by the curve $y=\dfrac{1}{x}+1$, the tangent at $\left( 2,\dfrac{3}{2} \right)$ and the line $x=1$ is
A. $\dfrac{4}{5}+\ln 2$
B. $-\dfrac{5}{4}+\ln 3$
C. $-\dfrac{5}{8}+\ln 2$
D. $\ln 2-\dfrac{5}{8}$

Answer 1

We first find the tangent of the curve $y=\dfrac{1}{x}+1$ at $\left( 2,\dfrac{3}{2} \right)$. We use the slope of the curve and find the three equations to place them in the graph. Then from the intersecting points we find the area and using integral form we find the solution.

Complete step by step answer:
The area is bounded by the curve $y=\dfrac{1}{x}+1$, the tangent at $A=\left( 2,\dfrac{3}{2} \right)$ and the line $x=1$.
We first need to find the equation of the tangent. We find the slope $\dfrac{dy}{dx}$ for the curve $y=\dfrac{1}{x}+1$
Differentiating the equation $y=\dfrac{1}{x}+1$ with respect to $x$, we get
$\begin{aligned} & y=\dfrac{1}{x}+1 \\\ & \Rightarrow \dfrac{dy}{dx}=-\dfrac{1}{{{x}^{2}}} \\\ \end{aligned}$
We find the slope value of the curve at $\left( 2,\dfrac{3}{2} \right)$ which is ${{\left[ \dfrac{dy}{dx} \right]}_{\left( 2,\dfrac{3}{2} \right)}}={{\left[ -\dfrac{1}{{{x}^{2}}} \right]}_{\left( 2,\dfrac{3}{2} \right)}}=-\dfrac{1}{4}$.
The equation of tangent is $\left( y-b \right)={{\left[ \dfrac{dy}{dx} \right]}_{\left( a,b \right)}}\left( x-a \right)$ where $\left( a,b \right)\equiv \left( 2,\dfrac{3}{2} \right)$.
$\begin{aligned} & \left( y-\dfrac{3}{2} \right)=\left[ -\dfrac{1}{4} \right]\left( x-2 \right) \\\ & \Rightarrow 4y-6=2-x \\\ & \Rightarrow x+4y=8 \\\ \end{aligned}$
Now we plot the graphs of $y=\dfrac{1}{x}+1$, $x+4y=8$ and $x=1$. The yellow marked area is the required one.

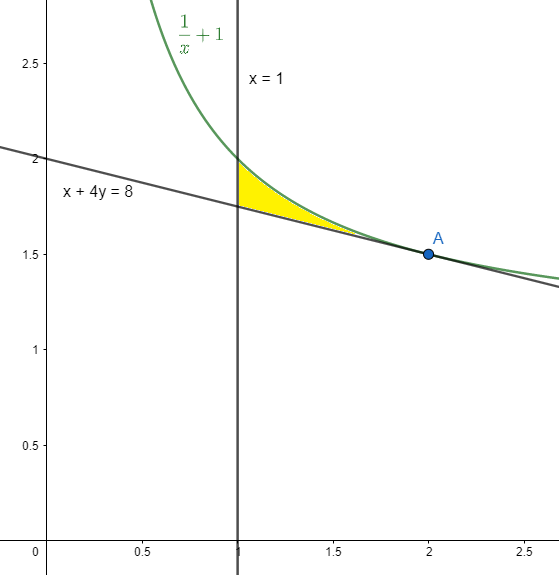
So, we subtract the area under the line $x+4y=8$ from the area under the curve $y=\dfrac{1}{x}+1$ to find the solution. The limit for the areas will be from $x=1$ to $x=2$.
We know that $x+4y=8$ which gives $y=\dfrac{8-x}{4}$
The integral form will be $\int\limits_{1}^{2}{\left( \dfrac{1}{x}+1 \right)dx}-\int\limits_{1}^{2}{\left( \dfrac{8-x}{4} \right)dx}=\int\limits_{1}^{2}{\left( \dfrac{1}{x}+1-\dfrac{8-x}{4} \right)dx}=\int\limits_{1}^{2}{\left( \dfrac{1}{x}-\dfrac{4-x}{4} \right)dx}$.
Integrating we get
$\begin{aligned} & \int\limits_{1}^{2}{\left( \dfrac{1}{x}-\dfrac{4-x}{4} \right)dx} \\\ & =\left[ \ln x-x+\dfrac{{{x}^{2}}}{8} \right]_{1}^{2} \\\ & =\left[ \ln 2-2+\dfrac{4}{8} \right]-\left[ \log 1-1+\dfrac{1}{8} \right] \\\ & =\ln 2-\dfrac{5}{8} \\\ \end{aligned}$

The correct option is D.

Note: we need to remember that the required area is bounded on the left side by the line $x=1$. The intersecting point of the line $x=1$ and $x+4y=8$ is $\left( 1,\dfrac{7}{4} \right)$. The area under a curve between two points is found out by doing a definite integral between the two points.