Question

Area of the region bounded by lines $y = - \dfrac{1}{2}x + 4$ , $x = 1$ ,$x = 5$ and X-axis is ……………
(A) 10
(B) 20
(C) 30
(D) 5

Answer 1

First, we will try to make the figure according to the equations given in the question, then we will find the point of intersections between the equations, then we will integrate the curve with its maximum or minimum limit. Hence, getting the final answer.

Complete step by step solution:
We will first consider the equation, $y = - \dfrac{1}{2}x + 4$
On multiplying by 2, we get
$\Rightarrow 2y = - x + 8$
Now, we get the three equations as
$2y = - x + 8$ , $x = 1$ , $x = 5$
Hence, now in the graph, we get

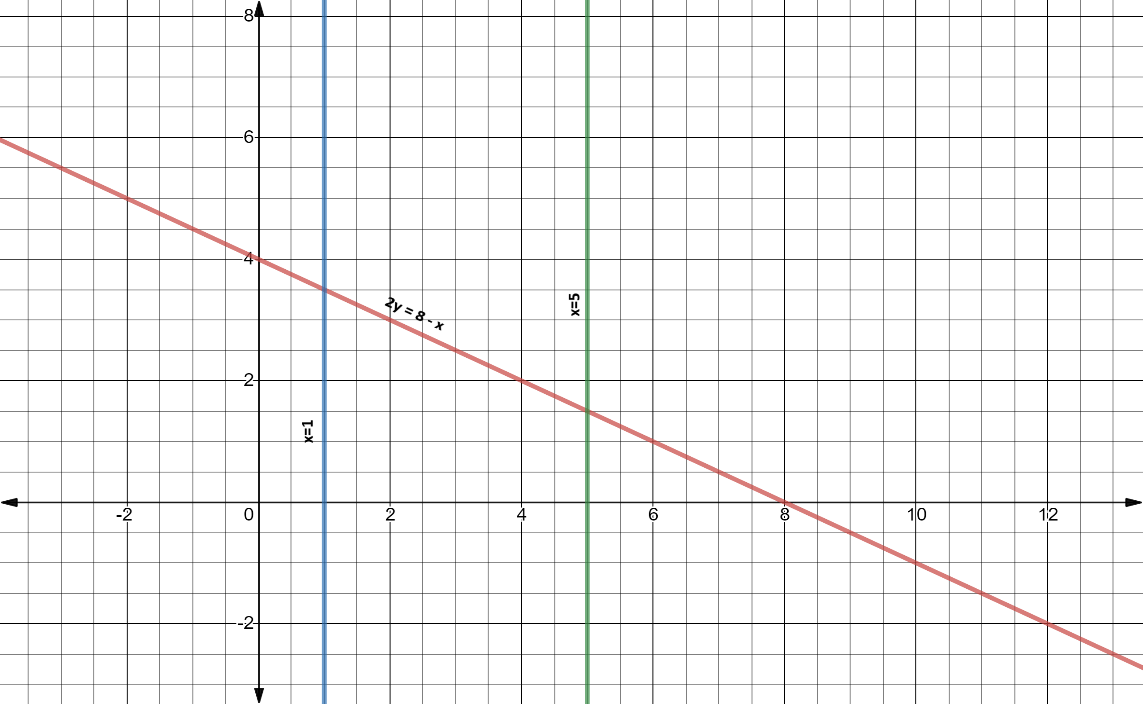
Now we know that the curve $2y = - x + 8$ is limited by the curves $x = 1$ and $x = 5$ .
Hence, to find the area, we will integrate the curve $y = \dfrac{{ - x + 8}}{2}$ with respect to x, having limits from 1 to 5, we get
Required area $= \int_1^5 {\dfrac{{ - x + 8}}{2}dx}$
On breaking the fraction into different terms, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \int_1^5 {\left( {\dfrac{{ - x}}{2} + \dfrac{8}{2}} \right)dx}$
Getting the fractions into its lowest form, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \int_1^5 {\left( {\dfrac{{ - x}}{2} + 4} \right)dx}$
Since we know that $\int_b^a {\left( {{f_1}(x) + {f_2}(x)} \right)dx} = \int_b^a {{f_1}(x)dx + \int_b^a {{f_2}(x)} dx}$ , hence
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \int_1^5 {\dfrac{{ - x}}{2}dx + \int_1^5 4 dx}$
Since we know that $\int_b^a {c \times f(x)dx = c\int_b^a {f(x)dx} }$ , hence
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \dfrac{{ - 1}}{2}\int_1^5 {xdx + 4\int_1^5 {dx} }$
We know that,
$\int_b^a {xdx = \left[ {\dfrac{{{x^2}}}{2}} \right]_b^a}$
$\int_b^a {dx = \left[ x \right]_b^a}$
Hence, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \dfrac{{ - 1}}{2}\left[ {\dfrac{{{x^2}}}{2}} \right]_1^5 + 4\left[ x \right]_1^5$
On substituting the value of limits, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \dfrac{{ - 1}}{2} \times \left( {\dfrac{{{5^2}}}{2} - \dfrac{{{1^2}}}{2}} \right) + 4 \times \left( {5 - 1} \right)$
Hence, solving for the bracket first, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \dfrac{{ - 1}}{2} \times \left( {\dfrac{{25}}{2} - \dfrac{1}{2}} \right) + 4 \times 4$
Solving further, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = \dfrac{{ - 1}}{2} \times \dfrac{{24}}{2} + 4 \times 4$
Now solving the products, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = - \dfrac{{24}}{4} + 4 \times 4$
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = - 6 + 16$
Hence, we get
$\Rightarrow \int_1^5 {\dfrac{{ - x + 8}}{2}dx} = 10$
Since the Required area is 10.
Hence, our final answer is (A).

Note:
In these questions, the limit of the integral is also defined by curves. We should very carefully define the limits of the integration of a curve as it is the trickiest part of the question, once defined, then it would be an easy task to evaluate the definite integral hence found.