Question

Area of the largest triangle that can be inscribed in a semicircle of the radius units is
(a) ${{r}^{2}}$ sq. units
(b) $\dfrac{1}{2}{{r}^{2}}$ sq. units
(c) $2{{r}^{2}}$ sq. units
(d) $\sqrt{2}{{r}^{2}}$ sq. units

Answer 1

In order to solve this problem, we need to know the formula for the area of the triangle. The area of the triangle is given by $\text{Area}=\dfrac{1}{2}\times \text{base}\times \text{height}$ . We first need to identify the base of the triangle, and then we need to vary the height and find the point that is farthest from the base. Also, there is a property of the semi-circle that says the angle inscribed in a semicircle is always a right angle.

Complete step-by-step answer :
We need to draw a triangle in the semicircle and we need to find the maximum area of the triangle.
Let’s imagine a triangle ABC inscribed in a triangle.

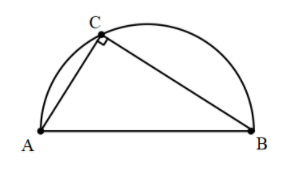
There is a property that says the angle inscribed in a semicircle is always a right angle.
Therefore, $\angle C={{90}^{\circ }}$ .
As we know that the base of the triangle is the diameter of the triangle.
Let the radius of the semicircle be r.
Then the base of the triangle becomes 2r.
The formula for the area of the triangle is given by $\text{Area}=\dfrac{1}{2}\times \text{base}\times \text{height}$ .
Substituting the value of base, we get,
$\text{Area}=\dfrac{1}{2}\times 2r\times \text{height}=r\times \text{height}$ .
The area of the triangle varies with respect to its perpendicular height from the base AB.
We need to find the point which is farthest from the base.
The farthest point from the base but still inscribed in the semicircle has to be the radius of the circle.
This is when the triangle will have the maximum height.
Therefore, we have height = r.
Now, the diagram with the maximum area looks as follows,

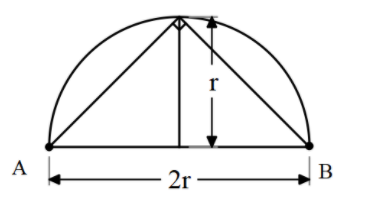
Substituting the values, we have,
$\text{Area}=r\times r={{r}^{2}}$ sq. units.
Hence, the correct option is (a).

Note : In this problem, we can also say the area of the maximum area of the triangle inscribed in the circle is also the same as of a semicircle. Because the base would be the same as the diameter of the circle and the farthest point is also the same that is the radius.