Question
Question: Area of the ellipse \(\frac { x ^ { 2 } } { a ^ { 2 } } + \frac { y ^ { 2 } } { b ^ { 2 } } = 1\) is...
Area of the ellipse a2x2+b2y2=1 is
A
πabsq. unit
B
21πabsq. unit
C
41πabsq. unit
D
None of these
Answer
πabsq. unit
Explanation
Solution
Since the given equation contains only even powers of x and only even powers of y, the curve is symmetrical about y-axis as well as x-axis.

∴ Whole area of given ellipse
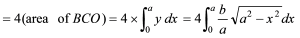
=4ab∫0π/2(21+cos2θ)dθ, {Putting x=asinθ}
=2ab(∫0π/2dθ+∫0π/2cos2θdθ)
=[θ]0π/2+[2sin2θ]0π/2=πabsq. unit.
