Solveeit Logo
Login

Question

Question: Area of parallelogram formed by the lines \[y = mx,y = mx + 1,y = nx\] and \[y = nx + 1\] equals to ...

Area of parallelogram formed by the lines y=mx,y=mx+1,y=nxy = mx,y = mx + 1,y = nx and y=nx+1y = nx + 1 equals to
A. ∣m+n∣(m−n)2\dfrac{{\left| {m + n} \right|}}{{{{\left( {m - n} \right)}^2}}}
B. 2∣m+n∣\dfrac{2}{{\left| {m + n} \right|}}
C. 1∣m+n∣\dfrac{1}{{\left| {m + n} \right|}}
D. 1∣m−n∣\dfrac{1}{{\left| {m - n} \right|}}

Explanation

Solution

In order to find the area of parallelogram first make the graph by the given lines then find the coordinates of the parallelogram and by using the formula of area of triangle which is given below we will proceed further.

Complete step-by-step answer:
Given lines are y=mx,y=mx+1,y=nxy = mx,y = mx + 1,y = nx and y=nx+1y = nx + 1. So, first we will make a graph as shown in the below:

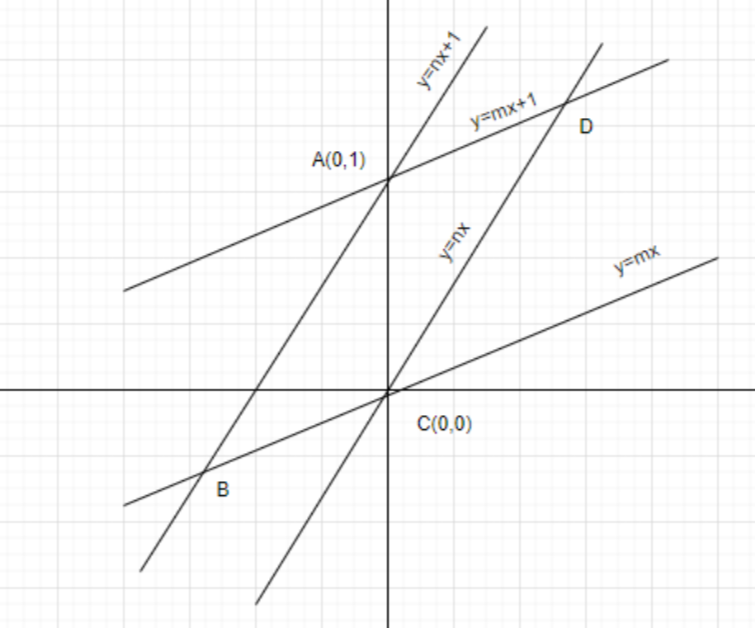
From figure we get the parallelogram ABCD, now we will find out its coordinate
Here A(0,1)A\left( {0,1} \right) and C(0,0)C\left( {0,0} \right)
For point B: The lines y=mxy = mx and y=nx+1y = nx + 1 intersect each other at a point B
So, we have

⇒mx=nx+1 ⇒x=1m−n  \Rightarrow mx = nx + 1 \\\ \Rightarrow x = \dfrac{1}{{m - n}} \\\

Substitute this value in the line y=mxy = mx, then we have
⇒y=mm−n\Rightarrow y = \dfrac{m}{{m - n}}
So, the coordinate of B is (1m−n,mm−n)\left( {\dfrac{1}{{m - n}},\dfrac{m}{{m - n}}} \right)
For D point: The two lines y=nxy = nx and y=mx+1y = mx + 1 intersects at a point D. So, we have

⇒nx=mx+1 ⇒x=1n−m  \Rightarrow nx = mx + 1 \\\ \Rightarrow x = \dfrac{1}{{n - m}} \\\

By substituting this value in the line y=nxy = nx, we have
⇒y=nn−m\Rightarrow y = \dfrac{n}{{n - m}}
So, the coordinate D is (1n−m,nn−m)\left( {\dfrac{1}{{n - m}},\dfrac{n}{{n - m}}} \right)
Therefore, coordinates of parallelogram ABCD are A(0,1),B(1m−n,mm−n),C(0,0)A\left( {0,1} \right),B\left( {\dfrac{1}{{m - n}},\dfrac{m}{{m - n}}} \right),C\left( {0,0} \right) and D(1n−m,nn−m)D\left( {\dfrac{1}{{n - m}},\dfrac{n}{{n - m}}} \right).
From the figure we have seen that area of parallelogram ABCD = 2×Area of ΔABC2 \times {\text{Area of }}\Delta {\text{ABC}}
We know that the area of ΔPQR\Delta PQR where, P(x1,y2),Q(x2,y2)P\left( {{x_1},{y_2}} \right),Q\left( {{x_2},{y_2}} \right) and R(x3,y3)R\left( {{x_3},{y_3}} \right) is

{{x_1}}&{{y_1}}&1 \\\ {{x_2}}&{{y_2}}&1 \\\ {{x_3}}&{{y_3}}&1 \end{array}} \right|$$ So, area of $$\Delta {\text{ABC}}$$ with $$A\left( {0,1} \right),B\left( {\dfrac{1}{{m - n}},\dfrac{m}{{m - n}}} \right),C\left( {0,0} \right)$$ is $$ \Rightarrow \Delta = \dfrac{1}{2}\left| {\begin{array}{*{20}{c}} 0&1&1 \\\ {\dfrac{1}{{m - n}}}&{\dfrac{m}{{m - n}}}&1 \\\ 0&0&1 \end{array}} \right|$$ Opening the determinant, we have

\Rightarrow \Delta = \dfrac{1}{2}\left| {\left[ {0 - \dfrac{1}{{m - n}} + 0} \right]} \right| \\
\therefore \Delta = \dfrac{1}{{2\left| {m - n} \right|}} \\

Therefore, area of $$\Delta ABC = \dfrac{1}{{2\left| {m - n} \right|}}$$ Hence, area of parallelogram ABCD =$$2 \times {\text{Area of }}\Delta {\text{ABC}}$$= $$2 \times \dfrac{1}{{2\left| {m - n} \right|}}$$ = $$\dfrac{1}{{\left| {m - n} \right|}}$$ **So, the correct answer is “Option A”.** **Note:** Students must remember the formula for finding the area of the triangle by determinant method. The determinant method is very handy to find the area of figure in coordinate geometry. The determinant is a scalar value that can be computed from the elements of a square matrix and encodes certain properties of the linear transformation described by the matrix. The determinant of a matrix A is denoted det A.