Question

Area of minor sector______.

Answer 1

Hint- This question is from circleS so first we will learn about circle and its parts.
Circle- A circle is a geometrical shape which is made up of an infinite number of points in a plane
that are located at a fixed distance from a point called as the center of the circle.
The fixed distance from any of these points to the center is known as the radius of the circle.

Complete step by step solution:
Sectors in circle- A sector is a portion of a circle which is enclosed between its two radii and the
arc joining them.
Like- a semi circle is also a sector with two radii as its diameter. It divides the whole circle in two equal parts or sectors. In this sector the angle between two radii is $180^\circ$.

But there are two types of sectors.
Major sector
Minor sector
The smaller area is known as the minor sector and the larger being the major sector.
In the diagram, $\theta$ is the central angle and “r” is the radius of the circle.

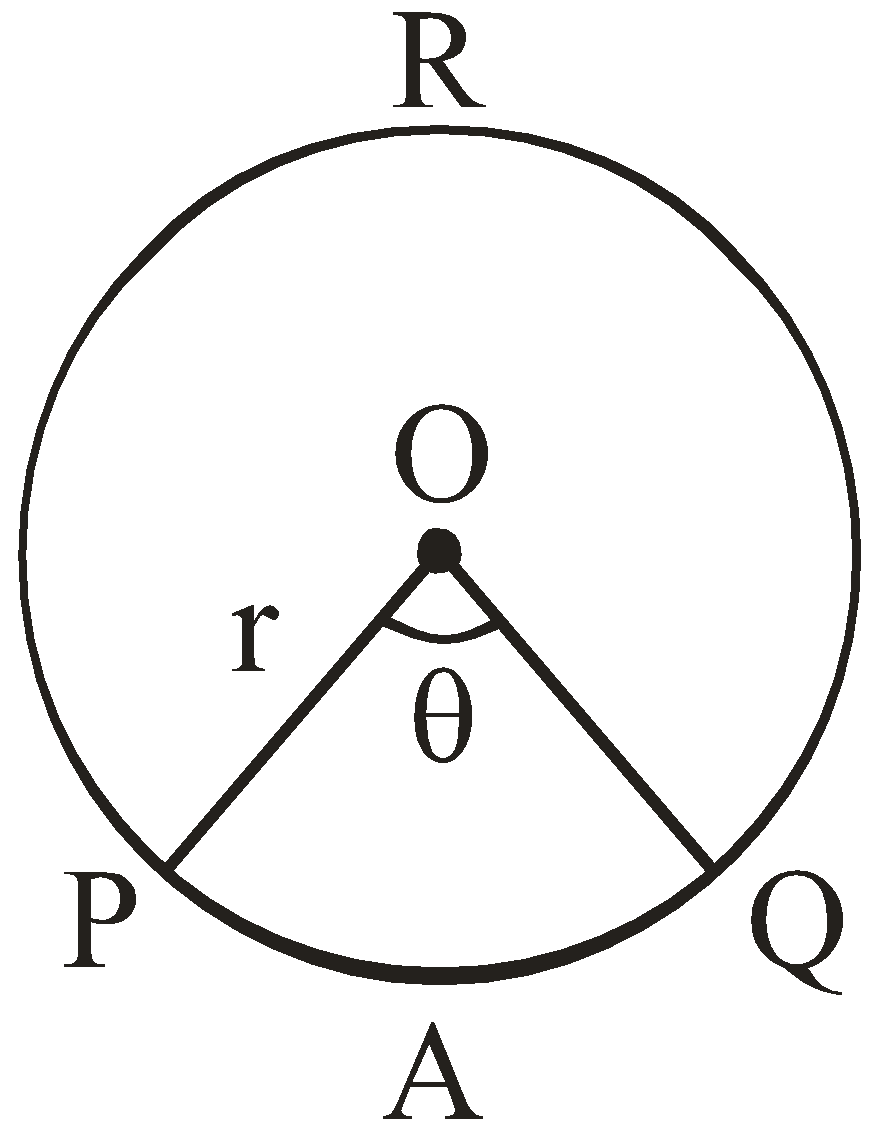
Here PAQO is a minor sector and PRQO is a major sector made by radius “r” and angle $\theta$.
Now in the next step we will learn how to calculate the area of sectors.
Step by step solution :
Keeping in mind that area of circle which is an angle of $360^\circ$ is $\pi {r^2}$.
We will calculate the area of sectors.
In the above circle with center O and radius r, let PAQO be a sector and $\theta$ (in degrees) be the angle of the sector.
When the angle is of $360^\circ$ area of the sector is $\pi {r^2}$.
So area of $1^\circ$ will be $\pi {r^2}/360^\circ$
therefore for the sector of angle $\theta$ area will be $\left( {\pi {r^2}/360^\circ } \right) \times \theta$
Or,
Area of minor sector PAQO is $= \theta \times \pi {r^2}$
Example radius
4 units, the angle of its sector is $45^\circ$
Area of sector $= \dfrac{\theta }{{360^\circ }} \times \pi {r^2}$
$= \dfrac{{45^\circ }}{{360^\circ }} \times \pi {r^2}$
$= 0.125 \times 3.14 \times {4^2} = 6.28$ sq. units

Note : 1. We can calculate the area of a semicircle by this formula of sector as we know that semicircle is also a sector with $180^\circ$ angle.
Area of sector $= \dfrac{\theta }{{360^\circ }} \times \pi {r^2}$
$= \dfrac{{180^\circ }}{{360^\circ }} \times \pi {r^2} = \dfrac{{\pi {r^2}}}{2}$
2. We can also calculate Area of major sector by subtracting area of minor sector from area of circle. i.e., $\pi {r^2} - \dfrac{\theta }{{360^\circ }} \times \pi {r^2}$