Solveeit Logo
Login

Question

Question: Area inside the parabola \({y^2} = 4ax\) between the lines \(x = a\,\& \,x = 4a\) is equal to \( ...

Area inside the parabola y2=4ax{y^2} = 4ax between the lines x=a & x=4ax = a\,\& \,x = 4a is equal to
a) 4a2 b) 8a2 c) 283a2 d) none of these  a) \,4{a^2} \\\ b) \,8{a^2} \\\ c) \,\dfrac{{28}}{3}{a^2} \\\ d) \,none\,of\,these \\\

Explanation

Solution

Area inside a parabola can be found using definite integration from x=a to x=4ax = a\,to\,x = 4a. As integration always gives area under the curve being represented. We have to integrate the function y=f(x)y = f(x)here y=4axy = \sqrt {4ax}
Area =∫a4af(x)dx= \int\limits_a^{4a} {f(x)dx}

Complete step-by-step answer:
Here, y=4axy = \sqrt {4ax}
Area =∫a4af(x)dx= \int\limits_a^{4a} {f(x)dx}
Area =∫a4a4axdx= \int\limits_a^{4a} {\sqrt {4ax} dx}
Area =4a∫a4axdx = \sqrt {4a} \int\limits_a^{4a} {\sqrt x } dx { 4a\sqrt {4a} is a constant and can be taken out of integration}
=4a[x12+112+1]a4a =4a[x3232]a4a =234a[(4a)32−(a)32] =234a[8(a)32−(a)32] =23×7(a)32×4a =283a2   sq units  = \sqrt {4a} \left[ {\dfrac{{{x^{\dfrac{1}{2} + 1}}}}{{\dfrac{1}{2} + 1}}} \right]_a^{4a} \\\ = \sqrt {4a} \left[ {\dfrac{{{x^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}}} \right]_a^{4a} \\\ = \dfrac{2}{3}\sqrt {4a} \left[ {{{\left( {4a} \right)}^{\dfrac{3}{2}}} - {{\left( a \right)}^{\dfrac{3}{2}}}} \right] \\\ = \dfrac{2}{3}\sqrt {4a} \left[ {8{{\left( a \right)}^{\dfrac{3}{2}}} - {{\left( a \right)}^{\dfrac{3}{2}}}} \right] \\\ = \dfrac{2}{3} \times 7{\left( a \right)^{\dfrac{3}{2}}} \times \sqrt {4a} \\\ = \dfrac{{28}}{3}{a^{2\,}}\,\,sq\,units \\\
Now this is the area of y=+4axy = + \sqrt {4ax} but not of y=−4axy = - \sqrt {4ax} which is also a solution of y2=4ax{y^2} = 4ax therefore to find the solution of either we can integrate or we can conclude that by symmetry it is also equal to =283a2   sq units = \dfrac{{28}}{3}{a^{2\,}}\,\,sq\,units
It can be clearly seen by the plot of y2=4ax{y^2} = 4ax

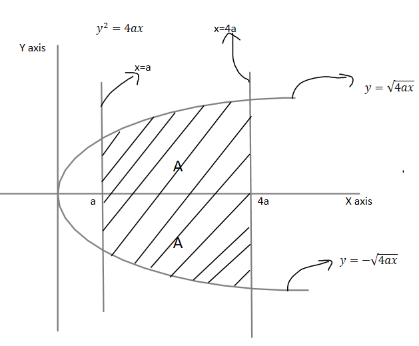
Total Area =A+A=2AA + A = 2A
Both graphs are symmetrical therefore total area equals to twice of area of y=+4axy = + \sqrt {4ax}
So total area of y2=4ax{y^2} = 4ax from x=a to x=4ax = a\,to\,x = 4a is equal to =2×283a2   sq units = 2 \times \dfrac{{28}}{3}{a^{2\,}}\,\,sq\,units =563a2  sq units = \dfrac{{56}}{3}{a^2}\,\,sq\,units
So option D is correct.

Note: We have to take both y=+4axy = + \sqrt {4ax} and y=−4axy = - \sqrt {4ax} into consideration while always solving remember to simplify the equation to y=f(x)y = f(x) as only it can be integrated don,t use y2=4ax{y^2} = 4ax to be integrated. Use y′=4axy' = \sqrt {4ax} to be integrated. On parabola take symmetry into account along the respective axis. On integration area comes out to be negative we take the absolute value of area we can integrate f(y)=y24af(y) = \dfrac{{{y^2}}}{{4a}} to find the same solution but the procedure becomes lengthy and we don’t use this method.