Question

Area enclosed by the graph of the function $y={{\ln }^{2}}x-1$ lying in the fourth quadrant is
[a] $\dfrac{2}{e}$
[b] $\dfrac{4}{e}$
[c] $2\left( e+\dfrac{1}{e} \right)$
[d] $4\left( e-\dfrac{1}{e} \right)$

Answer 1

Hint: Plot the curve on the graph paper. Identify the region whose area is to be found. Put y = 0 and solve for x in the equation of the curve to get the coordinates of the points at which it touches the x-axis. Hence prove that the area of the region is the area enclosed by the curve $y={{\ln }^{2}}x-1$, the x-axis and the ordinates $x=\dfrac{1}{e}$ and $x=e$. Use the fact that the area enclosed by the curve y =f(x), the x-axis and the ordinates x =a and x =b is given by $A=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$. Hence find the area of the curve enclosed in the fourth quadrant.

Complete step-by-step answer:

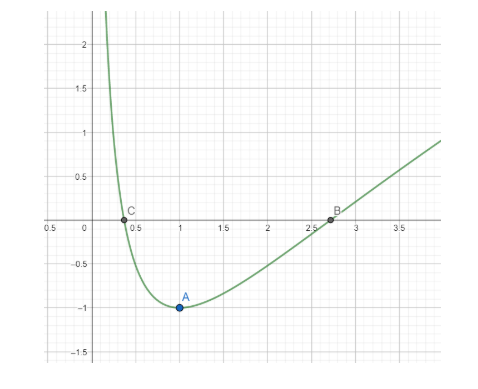
The graph of the curve is shown as above. The region enclosed by the curve in the fourth quadrant is the region ABCA.
Finding the coordinates of B and C:
At B and C, we have y = 0
Hence, we have
${{\ln }^{2}}x-1=0$
Adding 1 on both sides, we get
${{\ln }^{2}}x=1\Rightarrow \ln x=\pm 1$
We know that if $\ln x=a$, then $x={{e}^{a}}$
Hence, we have
$x={{e}^{-1}},{{e}^{1}}$
Hence, the coordinates of C are $\left( \dfrac{1}{e},0 \right)$ , and the coordinates of B are $\left( e,0 \right)$.
As is evident from the graph, the region ABCA is the region enclosed by the curve $y={{\ln }^{2}}x-1$, the x-axis and the ordinates $x=\dfrac{1}{e}$ and $x=e$
We know that the area enclosed by the curve y =f(x), the x-axis and the ordinates x =a and x =b is given by $A=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$.
Hence, we have
$A=\int_{\dfrac{1}{e}}^{e}{\left| {{\ln }^{2}}x-1 \right|dx}$
We know that in the interval $\left[ \dfrac{1}{e},e \right],{{\ln }^{2}}x-1\le 0$
Hence, we have
$A=\int_{\dfrac{1}{e}}^{e}{\left( 1-{{\ln }^{2}}x \right)dx}$
We know that $\int_{a}^{b}{\left( f\left( x \right)+g\left( x \right) \right)dx}=\int_{a}^{b}{f\left( x \right)dx}+\int_{a}^{b}{g\left( x \right)dx}$
Hence, we have
$A=\int_{\dfrac{1}{e}}^{e}{dx}-\int_{\dfrac{1}{e}}^{e}{{{\ln }^{2}}xdx}={{I}_{1}}-{{I}_{2}}$, where ${{I}_{1}}=\int_{\dfrac{1}{e}}^{e}{dx}$ and ${{I}_{2}}=\int_{\dfrac{1}{e}}^{e}{{{\ln }^{2}}xdx}$
Finding the value of ${{I}_{1}}$:
We know that $\int{dx}=x+C$
Hence, we have
${{I}_{1}}=\left. x \right|_{\dfrac{1}{e}}^{e}=e-\dfrac{1}{e}$
Finding the value of ${{I}_{2}}$:
Put ln x = t
Differentiating both sides, with respect to x, we get
$\dfrac{1}{x}dx=dt$
Hence, we have $dx=xdt={{e}^{t}}dt$
When $x=\dfrac{1}{e},t=\ln \left( \dfrac{1}{e} \right)=-1$ and when $x=e,t=\ln \left( x \right)=1$
Hence, we have
${{I}_{2}}=\int_{-1}^{1}{{{e}^{t}}\left( {{t}^{2}} \right)}dt$
Taking ${{t}^{2}}$ as first function and ${{e}^{t}}$ as second function and integrating by parts, we get
${{I}_{2}}=\left. {{t}^{2}}{{e}^{t}} \right|_{-1}^{1}-\int_{-1}^{1}{2t{{e}^{t}}dt}=e-\dfrac{1}{e}-\int_{-1}^{1}{2t{{e}^{t}}}dt$
Again integrating by parts taking t as first function and ${{e}^{t}}$ as second function, we get
${{I}_{2}}=e-\dfrac{1}{e}-\left. 2t{{e}^{t}} \right|_{-1}^{1}+2\int_{-1}^{1}{{{e}^{t}}dt}=e-\dfrac{1}{e}-2e-\dfrac{2}{e}+2\int_{-1}^{1}{{{e}^{t}}dt}$
Hence, we have
${{I}_{2}}=-e-\dfrac{3}{e}+2\left( \left. {{e}^{t}} \right|_{-1}^{1} \right)=-e-\dfrac{3}{e}+2e-\dfrac{2}{e}=e-\dfrac{5}{e}$
Hence, we have
$A=e-\dfrac{1}{e}-\left( e-\dfrac{5}{e} \right)=\dfrac{4}{e}$
Hence area enclosed by the curve $y={{\ln }^{2}}x-1$ in the fourth quadrant $=\dfrac{4}{e}$
Hence option [b] is correct.

Note: In this question, if we take horizontal strips instead of the vertical strips, the answer is going to be difficult to integrate and hence difficult to solve. Hence we should take care of which type of strips are going to make the solution easy. In this question, vertical strips made this solution of the question easy since y is expressed in terms of x.