Question

Area bounded by $y={{e}^{x}}$and lines $x=0$ and $y=e$ is given by:
This question has multiple correct answers.
1. $e-\int\limits_{0}^{1}{{{e}^{x}}dx}$
2. $e-\int\limits_{1}^{e}{\ln ydy}$
3. $e-1$
4. $1$

Answer 1

To find the area bounded by $y={{e}^{x}}$and lines $x=0$and $y=e$, students are required to first draw the plot graph of $y={{e}^{x}}$and lines also on the same graph and then find the points of intersection of the lines with the curve $y={{e}^{x}}$and then find area bounded by all the intersection points using the method of integration.

Complete step-by-step answer :
First, we will plot all the given curves and the lines on a single graph.

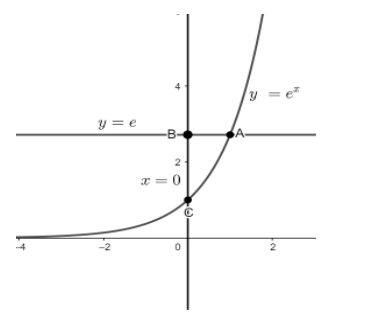
From the above graph we can see that $y={{e}^{x}}$ and the line $y=e$intersect at point A.
So, the coordinate of point A can be found by equating $y={{e}^{x}}$and $y=e$.
$\Rightarrow {{e}^{x}}=e$
$\therefore x=1$
Hence, y-coordinate of point A is e.
Hence, Point A is (1, e).
Coordinate of point B can be found by equating $x=0$and $y=e$ because they intersect at B.
So, point B will be (0, e)
Coordinate of point C can be found by equating $y={{e}^{x}}$and $x=0$ because they intersect at C.
So, point C will be (0, 1)
Since, the area bounded by curve $y={{e}^{x}}$and line $y=e$ and $x=0$is equal to the area bounded by intersecting points A, B, C.
Now, we will take a small vertical strip of width dx connecting the curve $y={{e}^{x}}$and the line $y=e$.
So, the total area bounded will be equal to the area traversed by vertical strip of width dx while moving it from the intersection point B where x-coordinate = 0 to point A where x-coordinate is 1.
So, $area=\int\limits_{0}^{1}{\left( e-{{e}^{x}} \right)dx}$, where $\left( e-{{e}^{x}} \right)$is the length of vertical strip at any point x. and dx is the width of that strip, and we know that multiplication of height and width gives the area.
$\Rightarrow \int\limits_{0}^{1}{edx-\int\limits_{0}^{1}{{{e}^{x}}dx}}$
$\Rightarrow e\int\limits_{0}^{1}{dx-\int\limits_{0}^{1}{\left( {{e}^{x}} \right)dx}}$
$\Rightarrow e-\int\limits_{0}^{1}{{{e}^{x}}dx}$
Hence, option (1) is our one of multiple answers.
We know that $\int{{{e}^{x}}dx={{e}^{x}}}+C$
$=e-\left( e-1 \right)$
$=e-e+1$
$=1$
Hence, option (4) is also our answer.
Now, instead of taking a vertical strip if we take a horizontal strip of width dy from the line $x=0$ to the curve $y={{e}^{x}}$ .
Now, express$y={{e}^{x}}$in terms of x:
$\Rightarrow y={{e}^{x}}$
Take ln both side:
$\Rightarrow \ln y=\ln {{e}^{x}}$
We know that $\ln {{e}^{x}}=x$.
So, $x=\ln y$
Hence, length of horizontal strip at point y on y-axis is given by: $\left( \ln y-0 \right)$
So, the total area bounded will be equal to the area traversed by horizontal strip of width dy while moving it from the point C where y-coordinate = 1 to point A where y-coordinate is e.
Hence, area bounded = $\int\limits_{1}^{e}{\left( \ln y-0 \right)dy}$ $=\int\limits_{1}^{e}{\ln ydy}$
We know that $\int{\ln xdx=x\ln x-x+C}$
Now, after putting the upper limit and the lower limit we will get:
=\left\\{ (e)\ln e-e \right\\}-\left\\{ 1\times \ln 1-1 \right\\}
$=e-e+1$
$=1$
Hence, option (1) and option (4) are only our required answer.

Note : The given question is a multiple-choice question, so students are required to check each and every possible option and try to express his/her answer in multiple forms and the form in which answer is given. Also, we should avoid making calculation errors while integrating, and taking limits.