Question

Area bounded by $y={{e}^{2x}}$ and lines x = 0, y = 0 and $x=\dfrac{e}{2}$ is given by
A. $\dfrac{1}{2}\int\limits_{0}^{2}{\ln ydy}$
B. $\dfrac{{{e}^{e}}-1}{2}$
C. ${{e}^{2}}$
D. None of these

Answer 1

Hint: First of all draw the area under the given curve to clearly visualize the question. Then, use $\int\limits_{a}^{b}{f(x)}={{e}^{2x}}$, a =0 and $b=\dfrac{e}{2}$.

Complete step-by-step answer:
Here we have to find the area bounded by $y={{e}^{2x}}$ and the lines x = 0, y = 0 and $x=\dfrac{e}{2}$. Before proceeding with the question, let us see how to find the area under a curve. Let the area be bounded by a curve, y = f(x), here the x-axis and the ordinates, x = a and x = b is given by $A=\int\limits_{a}^{b}{f(x)dx=\int\limits_{a}^{b}{ydx}}$.

Now, let us consider our question. Here let us first see the area under x = 0 and $x=\dfrac{e}{2}$ diagrammatically.

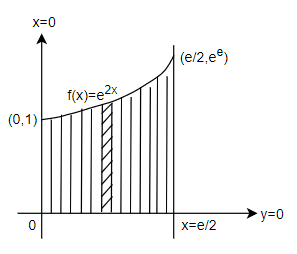
Basically, we have to find the shaded portion. So, we get the area as, $A=\int\limits_{a}^{b}{f(x)dx}$. By substituting$f(x)={{e}^{2x}}$, a = 0 and $b=\dfrac{e}{2}$ we get, $A=\int\limits_{0}^{\dfrac{e}{2}}{{{e}^{2x}}dx}$. We know that $\int\limits_{p}^{q}{{{e}^{ax}}}dx=\int\limits_{p}^{q}{\dfrac{{{e}^{ax}}}{a}}$. So we get, $A=\int\limits_{0}^{\dfrac{e}{2}}{\dfrac{{{e}^{2x}}}{2}dx}$
$A=\dfrac{1}{2}[{{e}^{2\left( \dfrac{e}{2} \right)}}-{{e}^{2\left( 0 \right)}}]$
$A=\dfrac{1}{2}\left( {{e}^{e}}-{{e}^{0}} \right)$
We know that ${{e}^{0}}=1$ so we get,
$A=\dfrac{1}{2}\left( {{e}^{e}}-1 \right)$
Hence, we get area between$y={{e}^{2x}}$, x = 0, y = 0 and $x=\dfrac{e}{2}$ as $\dfrac{1}{2}\left( {{e}^{e}}-1 \right)$ or $\dfrac{{{e}^{e}}-1}{2}$.
Therefore, option (B) is the correct answer.

Note: In this question, some students may make the mistake of taking ${{e}^{x}}$ instead of${{e}^{2x}}$, which is wrong, so the question must be read properly. Also, the students must note that the given formula is only for y = f(x) and that there is a slightly different formula for x = f(y). Also for y = f(x), we take vertical strips for the area under the curve while for x = f(y), we take horizontal strips for the area under the curve.