Question

Area bounded by the curve $y = \sin x$ between $x = 0$and $x = 2 \pi$ is

• A. 2 sq. unit
• B. 4 sq. unit
• C. 8 sq. unit
• D. None of these

Answer 1

Answer: (B)

4 sq. unit

Answer 2

We have $y = \sin x$

$x$	0	$\pi / 6$	$\pi / 2$	$\pi$	$3 \pi / 2$	$2 \pi$
$y$	0	0.5	1	0	–1	0

Join these points with a free hand to obtain a rough sketch

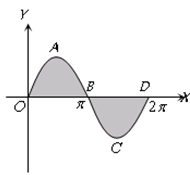
Required area = (area of $O A B$) + (area of$B C D )$

= $\int _ { 0 } ^ { \pi } y d x + \int _ { \pi } ^ { 2 \pi } ( - y ) d x$,

($\bullet \bullet$ Area $B C D$ is below $x -$axis)

= $\int _ { 0 } ^ { \pi } \sin x d x - \int _ { \pi } ^ { 2 \pi } \sin x d x = 4$ sq. unit.