Question

Area bounded by the curve y = log x, x – axis and the ordinates x = 1, x = 2 is
$\left( a \right)$ Log 4 sq. unit
$\left( b \right)$ Log (4) + 1sq. unit
$\left( c \right)$ Log (4) – 1sq. unit
$\left( d \right)$ None of these

Answer 1

Hint: In this particular type of question first draw the pictorial representation it will give us a clear picture of what we have to find out, and the formula for the area bounded by the curves is given as, ${\text{Area = }}\int\limits_{x = {x_1}}^{x = {x_2}} {\left( {{y_1} - {y_2}} \right)dx}$ so use these concepts to reach the solution of the question.

Complete step-by-step answer:

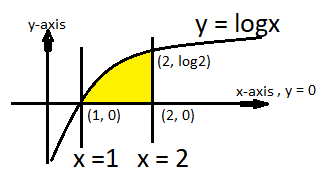
The area bounded by the curves, y = log x, x – axis and the ordinates x = 1, x = 2 is shown above in the figure by yellow color.
So we have to find out this highlighted area.
Now the area bounded by the curves is given as,
$\Rightarrow {\text{Area = }}\int\limits_{x = {x_1}}^{x = {x_2}} {\left( {{y_1} - {y_2}} \right)dx}$................. (1)
Where (${y_1}$) is the upper curve and (${y_2}$) is the lower curve and ${x_1},{x_2}$ are the initial and final limits of the integration.
Now, (${y_1}$) = log x and (${y_2}$) = 0 (x –axis), and, ${x_1} = 1,{x_2} = 2$
Now substitute these values in equation (1) so the area bounded by the curves is,
$\Rightarrow {\text{Area = }}\int\limits_{x = 1}^{x = 2} {\left( {\log x - 0} \right)dx}$
Now we solve this integration by parts,
$\Rightarrow {\text{Area = }}\int\limits_{x = 1}^{x = 2} {1.\log xdx}$............ (2)
Where log x is considered as 2nd function and 1 is considered as 1st function.
$\Rightarrow \int {{1^{st}}{{.2}^{nd}}dx} = {2^{nd}}\int {{1^{st}}dx} - \int {\left( {\left( {\dfrac{d}{{dx}}{2^{nd}}} \right)\int {{1^{st}}dx} } \right)dx} + C$, where C is some integration constant.
$\Rightarrow {\text{Area = }}\left[ {\log x\int {1dx} } \right]_1^2 - \int\limits_1^2 {\left( {\left( {\dfrac{d}{{dx}}\log x} \right)\int {1dx} } \right)dx}$
Now as we know that integration of constant (i.e. 1) w.r.t x is nothing but x, and differentiation of log x w.r.t x is (1/x), so we have,
$\Rightarrow {\text{Area = }}\left[ {x\log x} \right]_1^2 - \int\limits_1^2 {\left( {\left( {\dfrac{1}{x}} \right)x} \right)dx}$
$\Rightarrow {\text{Area = }}\left[ {x\log x} \right]_1^2 - \int\limits_1^2 {\left( 1 \right)dx}$
$\Rightarrow {\text{Area = }}\left[ {x\log x} \right]_1^2 - \left[ x \right]_1^2$
Now apply the integration limits we have,
$\Rightarrow {\text{Area = }}\left[ {2\log 2 - 1\log 1} \right] - \left[ {2 - 1} \right]$
As we know the value of log1 = 0 and $a\log b = \log {b^a}$ so we have,
$\Rightarrow {\text{Area = }}\left[ {\log {2^2} - 0} \right] - \left[ 1 \right]$
$\Rightarrow {\text{Area}} = \left( {\log 4 - 1} \right)$ Sq. unit
So this is the required answer.
Hence option (C) is the correct answer.

Note – Whenever we face such types of questions the key concept we have to remember is that always recall how to plot the log x otherwise we cannot plot the area bounded by the given curves, so after plotting the curves as above highlight the area as above, then apply integration formula of area bounded by the curve and simplify as above we will get the required answer.