Question

APPOINTMENTS/MEETINGS

8 AM 2

°F 10

$\theta$

$\mu = 0$

value of F such that block is at rest.

Answer 1

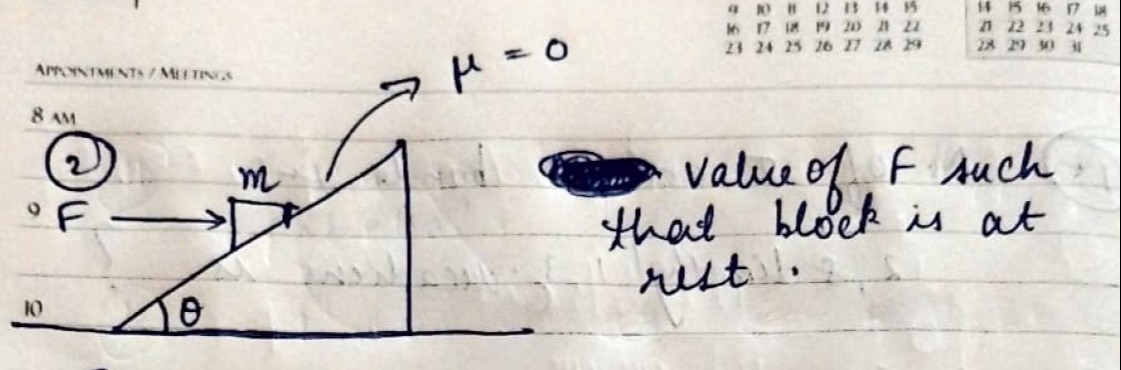
F = mg \tan \theta

Answer 2

The problem asks for the value of force F such that the block 'm' remains at rest on the inclined plane. The inclined plane is also subject to the force F. The problem states $\mu = 0$, meaning all surfaces are frictionless.

Let 'a' be the horizontal acceleration of the wedge (inclined plane) to the right. Since the block 'm' is at rest relative to the wedge, it also moves with the same horizontal acceleration 'a' with respect to the ground.

We can analyze the forces acting on the block 'm' using either an inertial frame (ground frame) or a non-inertial frame (frame of the wedge).

Method 1: Using an inertial frame (ground frame)

The forces acting on the block 'm' are:

1. Gravity: $mg$ acting vertically downwards.
2. Normal force: $N$ from the inclined surface, acting perpendicular to the surface.

Since the block is at rest relative to the wedge, its vertical acceleration is zero, and its horizontal acceleration is 'a'.

Resolve the forces into horizontal and vertical components:

• The normal force $N$ makes an angle $\theta$ with the vertical.
• The gravitational force $mg$ is entirely vertical.

Applying Newton's second law: Vertical equilibrium: The net vertical force is zero. $N \cos \theta - mg = 0$ $N = \frac{mg}{\cos \theta}$ (Equation 1)

Horizontal motion: The net horizontal force causes acceleration 'a'. $N \sin \theta = ma$ (Equation 2)

Substitute the expression for $N$ from Equation 1 into Equation 2: $\left(\frac{mg}{\cos \theta}\right) \sin \theta = ma$ $mg \tan \theta = ma$ $a = g \tan \theta$

This is the required horizontal acceleration of the wedge (and the block) for the block to remain at rest relative to the wedge.

Now, consider the system of the wedge and the block. Let the mass of the wedge be $M_{wedge}$. The total mass of the system is $(M_{wedge} + m)$. The external horizontal force acting on this system is F.

Applying Newton's second law for the combined system: $F = (M_{wedge} + m) a$

Substitute the expression for 'a': $F = (M_{wedge} + m) g \tan \theta$

Discussion on $M_{wedge}$: The problem statement does not provide the mass of the wedge ($M_{wedge}$). If a numerical value for F is expected, this indicates either:

1. The question implicitly assumes the wedge is massless (i.e., $M_{wedge} = 0$). In this case, $F = mg \tan \theta$.
2. The question expects the answer in terms of $M_{wedge}$, $m$, $g$, and $\theta$.
3. There is missing information.

Given that similar problems often provide masses for both the block and the wedge, and the force F is shown acting on the wedge, the most complete physical answer involves $M_{wedge}$. However, in the absence of $M_{wedge}$, if a single expression in terms of 'm' and 'g' is expected, it usually implies that the force F is directly applied to the block on a fixed wedge, or the wedge is massless.

If F were applied directly to the block on a fixed wedge, for the block to be at rest, the component of F along the incline must balance the component of gravity along the incline: $F \cos \theta = mg \sin \theta$, which leads to $F = mg \tan \theta$. This is the same result as assuming a massless wedge in the original setup.

Without further information or clarification on $M_{wedge}$, the most common interpretation in such scenarios where the wedge's mass is not given and a definite answer in terms of 'm' is expected is that the applied force F is the one required to provide the necessary acceleration for the block itself, or that the wedge is massless. Both lead to the same expression.

Therefore, assuming the simplest case that allows for an answer dependent only on 'm', 'g', and '$\theta$': $F = mg \tan \theta$

The question asks for the "value of F such that block is at rest." This value is $mg \tan \theta$.