Question

A metallic sphere floats in an immiscible mixture of water ($\rho_w$ = 10³ kg/m³) and a liquid ($\rho_L$ = 13.5 x 10³) with (1/5)th portion by volume in the liquid and remaining in water. The density of the metal is :

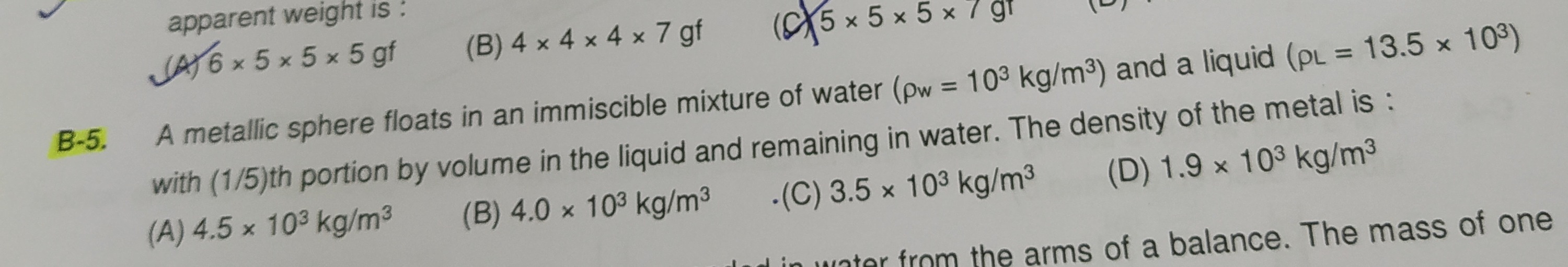
• A. 4.5 x 10³ kg/m³
• B. 4.0 x 10³ kg/m³
• C. 3.5 x 10³ kg/m³
• D. 1.9 x 10³ kg/m³

Answer 1

Answer: (C)

3.5 x 10³ kg/m³

Answer 2

Let $V$ be the total volume of the sphere and $\rho_m$ be its density.

Volume in liquid $V_L = \frac{1}{5}V$.

Volume in water $V_w = (1 - \frac{1}{5})V = \frac{4}{5}V$.

For a floating body, the weight of the body equals the total buoyant force.

Weight of sphere $W = \rho_m V g$.

Total buoyant force $F_B = F_{Bw} + F_{BL} = \rho_w V_w g + \rho_L V_L g$.

Equating weight and buoyant force:

$\rho_m V g = \rho_w (\frac{4}{5}V) g + \rho_L (\frac{1}{5}V) g$

Dividing by $Vg$:

$\rho_m = \rho_w \frac{4}{5} + \rho_L \frac{1}{5}$

Substitute the given densities:

$\rho_m = (10^3 \text{ kg/m}^3) \frac{4}{5} + (13.5 \times 10^3 \text{ kg/m}^3) \frac{1}{5}$

$\rho_m = 0.8 \times 10^3 + 2.7 \times 10^3$

$\rho_m = (0.8 + 2.7) \times 10^3$

$\rho_m = 3.5 \times 10^3 \text{ kg/m}^3$