Question

AP & BP are tangents to the parabola ${y^2} = 4x$ at A & B. If the chord AB passes through a fixed point $\left( { - 1,1} \right)$, then the equation of the locus of P is
A.$y = 2\left( {x - 1} \right)$
B.$y = 2\left( {x + 1} \right)$
C.$y = 2x$
D.${y^2} = 2\left( {x - 1} \right)$

Answer 1

Let us assume the coordinates of the point P is represented by $\left( {h,k} \right)$ . We can formulate the equation for $\left( {h,k} \right)$ by finding the equation for the chord of contact AB with respect to P. The equation for the chord of the contact is $T = 0$, where $T$ is given by replacing $y$ with $y{y_1}$ and $x$ with $\dfrac{{x + {x_1}}}{2}$ for the parabola ${y^2} = 4ax$.

Complete step-by-step answer:
Let us assume the coordinates of the point P is given by the $\left( {h,k} \right)$.
Let us draw the figure according to the condition given in the question.

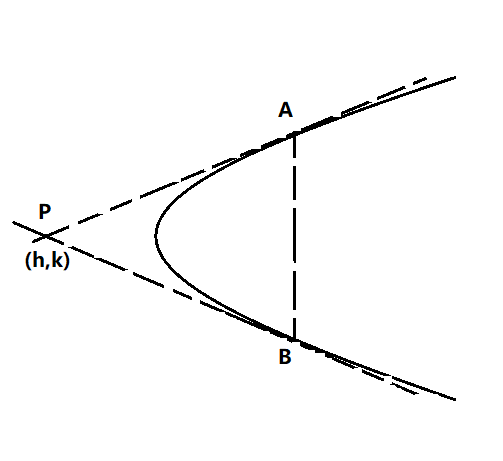
Here, AP and BP are the tangents to the parabola ${y^2} = 4x$ at the points A and B.
The equation of the chord AB is given by the equation of the chord of the contact with respect to the point P.
$T = 0$
The equation $T$ is formed by replacing $y$ with $y{y_1}$ and $x$ with $\dfrac{{x + {x_1}}}{2}$ in the equation for the parabola ${y^2} = 4x$. Here, $\left( {{x_1},{y_1}} \right)$ are the coordinates of the point of the intersection of the tangents to the parabola.
According to the question, the point of intersection of the tangents to the parabola is given by the coordinates of point P, that is $\left( {h,k} \right)$.
Thus replacing $y$ with $yk$ and $x$ with $\dfrac{{x + h}}{2}$ in the equation for the parabola ${y^2} = 4x$, we get
$ky = 4\left( {\dfrac{{x + h}}{2}} \right)$
The equation $ky = 4\left( {\dfrac{{x + h}}{2}} \right)$ represents the equation for the chord AB. It is given that the chord AB is passing through the fixed point $\left( { - 1,1} \right)$. Thus replacing $x$ with $- 1$ and $y$ with 1 in the equation $ky = 4\left( {\dfrac{{x + h}}{2}} \right)$, we get
$k.1 = 4\left( {\dfrac{{ - 1 + h}}{2}} \right)$
We can simplify the above equation as
$k = 2\left( {h - 1} \right)$
The above relation defines the locus of the point P.
Replacing $h$ with $x$ and $k$with y, we get
$y = 2\left( {x - 1} \right)$
Thus option A is the correct answer.

Note: The chord of contact is the chord joining the points of contact of the tangent to the parabola from a common external point. The equation for the chord of contact is of the form $T = 0$ for the parabola. The chord of contact is also defined for other conic figures such as circles.