Question
Question: Answer the following question in one word or one sentence or as per exact requirement of the questio...
Answer the following question in one word or one sentence or as per exact requirement of the question.
If A = {(x, y): y =ex, x ϵ R} and B = {(x, y): y =e - x, x ϵ R}, then write A ∩ B.
Solution
Hint: To determine the answer, we write the definition of A ∩ B using the given A and B. Then we perform the calculations to get the values of x and y. Definition of A ∩ B states that the set of elements which are common in both sets A and B.
Complete step-by-step solution -
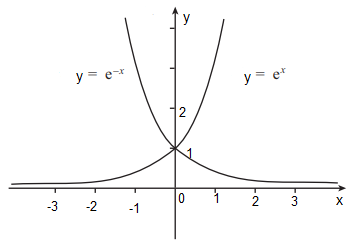
We need: A ∩ B
⟹ {(x, y): y =ex, x ϵ R} ∩ {(x, y): y =e - x, x ϵ R}
⟹ {(x, y): y =ex∩ e - x, x ϵ R}
The intersection of exand e - xis nothing but,
⟹ex=e - x
Applying ln on both sides we get,
⟹ln ex= ln e - x
We know ln (ex) = x ln e = x (1) = x -- ln (e) = 1, logarithmic identity.
⟹x = -x
⟹2x = 0
⟹x = 0
Therefore, ex= e - x= e0= 1
Hence y = 1.
At x = 0, y = 1
Therefore, A ∩ B = {(0, 1)} is a singleton set.
Note: The key in such problems is to understand the definition of A ∩ B using the given A and B. A intersection B refers to a common solution set of A and B. Using the correct operations, like applying the log function to reduce the equations and finding the values of x and y is a crucial step.
Any number to the power of 0 is 1. e is a numerical constant with a value of 2.71828.
