Question

Answer Q.49, Q.50 and Q.51 by appropriately matching the information given in the three columns of the following table.

Let S = 0 be the parabola touching x-axis at (1, 0) and y = x at (1, 1)

	Column-1		Column-II		Column-III
(P)	If slope of the axis of the parabola is $\frac{a}{b}$, (H.C.F(a, b)=1) then	(I)	a - b equals	(i)	1
(Q)	If focus of the parabola is (a, b) then	(II)	a + b equals	(ii)	4
(R)	If equation of the directrix of the parabola is ax + by = 1 then	(III)	5(a + b) equals	(iii)	7
(S)	If foot of the directrix of the parabola is (a, b) then	(IV)	$\frac{25}{2}$(a+b) equals	(iv)	3

9. Which of the following is the only CORRECT combination?

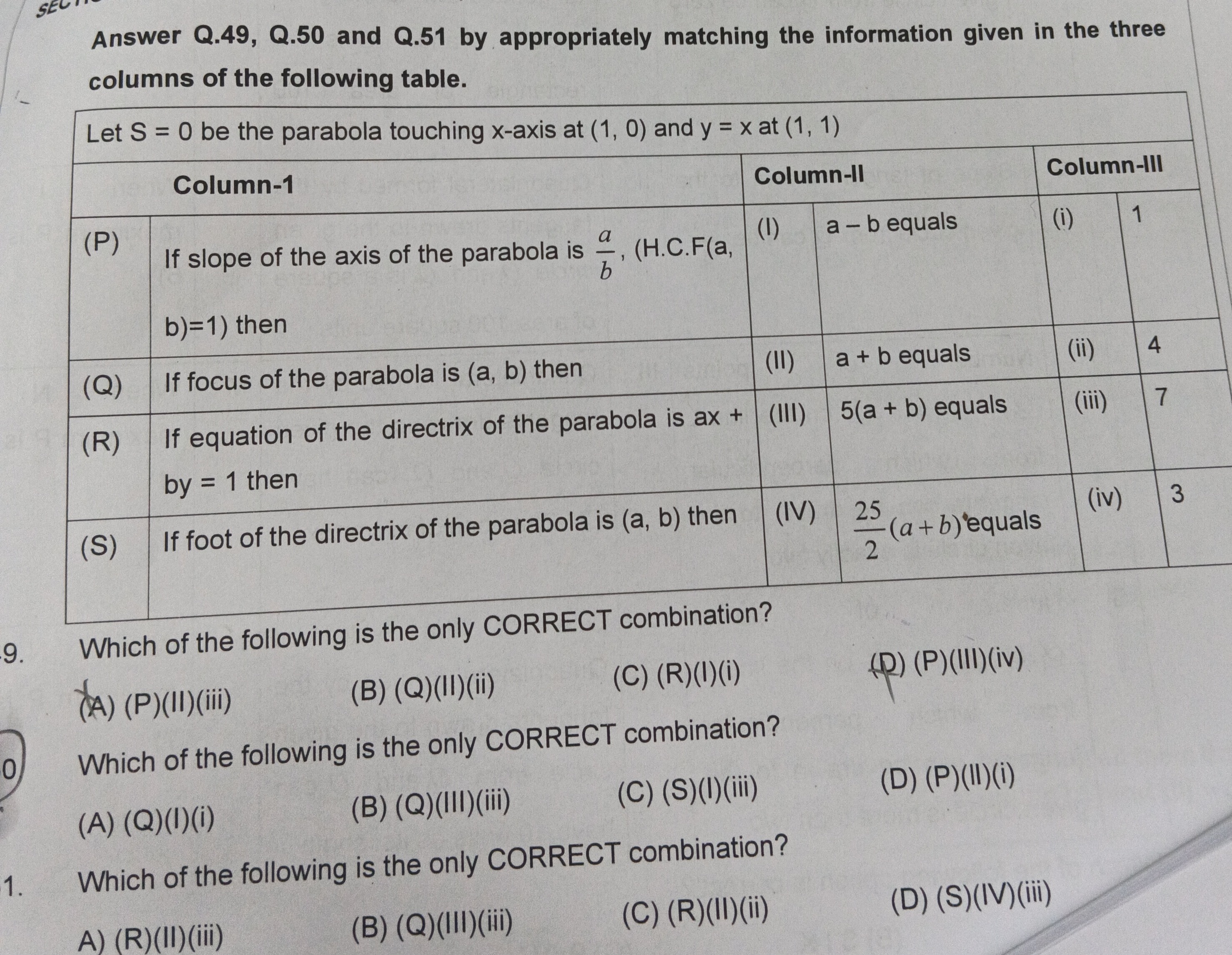
• A. (P)(II)(iii)
• B. (Q)(II)(ii)
• C. (R)(I)(i)
• D. (P)(III)(iv)

Answer 1

None of the options are correct.

Answer 2

1. Equation of the Parabola: The parabola touches the x-axis ($L_1: y=0$) at (1, 0) and the line $y=x$ ($L_2: x-y=0$) at (1, 1). The chord of contact $C$ passes through (1, 0) and (1, 1), so its equation is $x=1$ ($C: x-1=0$). The equation of the parabola is given by $L_1 L_2 = \lambda C^2$. $y(x-y) = \lambda (x-1)^2$ $xy - y^2 = \lambda (x^2 - 2x + 1)$ $\lambda x^2 - xy + y^2 - 2\lambda x + \lambda = 0$. For this to be a parabola, the condition $h^2 = ab$ must be satisfied, where $a=\lambda$, $b=1$, $h=-1/2$. $(-1/2)^2 = \lambda \cdot 1 \implies \lambda = 1/4$. Substituting $\lambda=1/4$, the equation of the parabola is: $\frac{1}{4}x^2 - xy + y^2 - \frac{1}{2}x + \frac{1}{4} = 0$ Multiplying by 4: $x^2 - 4xy + 4y^2 - 2x + 1 = 0$.

2. Slope of the Axis (P): The line joining the point of intersection of the two tangents $y=0$ and $x-y=0$ (which is $P(0,0)$) to the midpoint of their chord of contact $AB$ (which is $M(\frac{1+1}{2}, \frac{0+1}{2}) = M(1, 1/2)$) is parallel to the axis of the parabola. The slope of the line $PM$ is $\frac{1/2 - 0}{1 - 0} = 1/2$. Therefore, the slope of the axis of the parabola is $1/2$. For (P), the slope is $\frac{a}{b}$, where H.C.F(a, b)=1. So $a=1, b=2$. (P)(I) $a-b = 1-2 = -1$. (P)(II) $a+b = 1+2 = 3$. (P)(III) $5(a+b) = 5(3) = 15$. (P)(IV) $\frac{25}{2}(a+b) = \frac{25}{2}(3) = \frac{75}{2}$.

3. Focus (Q) and Directrix (R) and Foot of Directrix (S): The equation of the parabola is $x^2 - 4xy + 4y^2 - 2x + 1 = 0$. This can be written as $(x-2y)^2 = 2x-1$. Let the focus be $(x_f, y_f)$ and the directrix be $Ax+By+C=0$. The equation of the parabola is $(x-x_f)^2+(y-y_f)^2 = \frac{(Ax+By+C)^2}{A^2+B^2}$. By comparing coefficients with $x^2 - 4xy + 4y^2 - 2x + 1 = 0$, we find that the axis is $x-2y-1=0$. The directrix must be perpendicular to the axis, so its equation is $2x+y+d=0$. The focus $(x_f, y_f)$ lies on the axis $x-2y-1=0$, so $x_f = 2y_f+1$. Let $y_f=k$, so $x_f=2k+1$. Substituting into the parabola equation: $5((x-(2k+1))^2+(y-k)^2) = (2x+y+d)^2$. $5(x^2-2x(2k+1)+(2k+1)^2+y^2-2ky+k^2) = 4x^2+y^2+d^2+4xy+4dx+2dy$. $x^2+4y^2-4xy - (2(2k+1)+4d)x - (2k+2d)y + (5((2k+1)^2+k^2)-d^2) = 0$. Comparing with $x^2 - 4xy + 4y^2 - 2x + 1 = 0$: Coefficient of $x$: $-(2(2k+1)+4d) = -2 \implies 4k+2+4d=2 \implies 4k+4d=0 \implies k+d=0 \implies d=-k$. Coefficient of $y$: $-(2k+2d) = 0 \implies 2k+2d=0 \implies k+d=0$. (Consistent) Constant term: $5((2k+1)^2+k^2)-d^2 = 1$. $5(4k^2+4k+1+k^2)-(-k)^2 = 1$. $5(5k^2+4k+1)-k^2 = 1$. $25k^2+20k+5-k^2 = 1$. $24k^2+20k+4 = 0$. $6k^2+5k+1 = 0$. Factoring: $(3k+1)(2k+1) = 0$. This gives two possible values for $k$: $k=-1/3$ or $k=-1/2$.

   Case 1: $k=-1/3$ $d=-k=1/3$. Focus $(a,b) = (2k+1, k) = (2(-1/3)+1, -1/3) = (1/3, -1/3)$. Directrix $2x+y+1/3=0 \implies 6x+3y+1=0$. For $ax+by=1$, $a=6, b=3$. Foot of directrix: Intersection of axis $x-2y-1=0$ and directrix $6x+3y+1=0$. Solving $x=2y+1$: $6(2y+1)+3y+1=0 \implies 12y+6+3y+1=0 \implies 15y=-7 \implies y=-7/15$. $x=2(-7/15)+1 = -14/15+1 = 1/15$. Foot of directrix $(a,b) = (1/15, -7/15)$.

   Case 2: $k=-1/2$ $d=-k=1/2$. Focus $(a,b) = (2k+1, k) = (2(-1/2)+1, -1/2) = (0, -1/2)$. Directrix $2x+y+1/2=0 \implies 4x+2y+1=0$. For $ax+by=1$, $a=4, b=2$. Foot of directrix: Intersection of axis $x-2y-1=0$ and directrix $4x+2y+1=0$. Solving $x=2y+1$: $4(2y+1)+2y+1=0 \implies 8y+4+2y+1=0 \implies 10y=-5 \implies y=-1/2$. $x=2(-1/2)+1 = -1+1 = 0$. Foot of directrix $(a,b) = (0, -1/2)$.

4. Evaluate Options:

   Q.49: (A) (P)(II)(iii): (P) $a+b=3$. (iii) 7. $3=7$. (Incorrect) (B) (Q)(II)(ii): (Q) $a+b$. (ii) 4. Case 1: $1/3+(-1/3)=0$. Case 2: $0+(-1/2)=-1/2$. Neither is 4. (Incorrect) (C) (R)(I)(i): (R) $a-b$. (i) 1. Case 1: $6-3=3$. Case 2: $4-2=2$. Neither is 1. (Incorrect) (D) (P)(III)(iv): (P) $5(a+b)=15$. (iv) 3. $15=3$. (Incorrect) Based on calculations, none of the options for Q.49 are correct.