Solveeit Logo
Login

Question

Question: Angle between the tangents drawn to \({x^2} + {y^2} - 2x - 4y + 1 = 0\) at the points where it is cu...

Angle between the tangents drawn to x2+y2−2x−4y+1=0{x^2} + {y^2} - 2x - 4y + 1 = 0 at the points where it is cut by the liney=2x+c  is  π2 y = 2x + c\,\,{\text{is}}\,\,\dfrac{\pi }{2}\,then,
A). ∣c∣=5|{\text{c}}| = \sqrt 5
B). ∣c∣=25|{\text{c}}| = 2\sqrt 5
C). ∣c∣=10|{\text{c}}| = \sqrt {10}
D). ∣c∣=210|{\text{c}}| = 2\sqrt {10}

Explanation

Solution

Given the equation of the circle from the angle between the tangent is drawnx2+y2−2x−4y+1=0{x^2} + {y^2} - 2x - 4y + 1 = 0 is in the general form.
Therefore, use the formula (x−h)2+(y−k)2=r2{(x - h)^2} + {(y - k)^2} = {r^2} to find the center and
radius of the given circle. Use the concept of the distance of the point (x1,  y1)({x_1},\,\,{y_1}) to the line Ax1+By1+c=0A{x_1} + B{y_1} + c = 0 , that is d=∣Ax1+By1+c∣A2+B2d = \dfrac{{|A{x_1} + B{y_1} + c|}}{{\sqrt {{A^2} + {B^2}} }}, using all this information we need to find the value of the constant c.

Complete step-by-step solution:

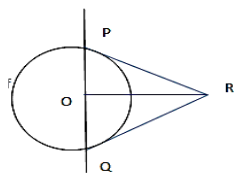
Given the equation of circle x2+y2−2x−4y+1=0{x^2} + {y^2} - 2x - 4y + 1 = 0 and the circle cut by the line y=2x+c  y = 2x + c\,\,. Draw the tangents at the point of intersection of the circle and the line.
Also given that the angle between the tangents drawn at the points
Where the line cuts the circle is 900{90^0} .
Therefore the tangents are perpendicular to each other
x2+y2−2x−4y+1=0{x^2} + {y^2} - 2x - 4y + 1 = 0
By completing the square method
x2−2x+1−1+y2−4y+4−4+1=0{x^2} - 2x + 1 - 1 + {y^2} - 4y + 4 - 4 + 1 = 0
(x−1)2+(y−2)2−4=0{(x - 1)^2} + {(y - 2)^2} - 4 = 0
(x−1)2+(y−2)2=4{(x - 1)^2} + {(y - 2)^2} = 4
Compare this equation with (x−h)2+(y−k)2=r2{(x - h)^2} + {(y - k)^2} = {r^2} the center of this equation is (h, k) and radius is r.
Therefore, we get Centre is (1, 2)\left( {1,{\text{ }}2} \right) and radius is 22 .
From the diagram angle PRQ =900 = {90^0} (given)
Join OR so that the angles PRO and QRO equal to 450{45^0}.
Therefore OR = 2 cos450= 2OR{\text{ }} = {\text{ }}2{\text{ }}cos{45^0} = {\text{ }}2 .12=2\dfrac{1}{{\sqrt 2 }} = \sqrt 2
Now consider the line y=2x+c  ⇒2x−y+c=0y = 2x + c\,\, \Rightarrow 2x - y + c = 0
We know that the perpendicular distance from the point (x1,  y1)({x_1},\,\,{y_1}) to the line Ax1+By1+c=0A{x_1} + B{y_1} + c = 0 is
d=∣Ax1+By1+c∣A2+B2d = \dfrac{{|A{x_1} + B{y_1} + c|}}{{\sqrt {{A^2} + {B^2}} }}
Therefore, the perpendicular distance from (1, 2) to the line 2x−y+c=02x - y + c = 0 is the radius.
Perpendicular distance = ∣2(1)−1(2)+c∣12+22\dfrac{{|2(1) - 1(2) + c|}}{{\sqrt {{1^2} + {2^2}} }}
2=∣c∣5⇒∣c∣=10\sqrt{2} = \dfrac{{|c|}}{{\sqrt 5 }} \Rightarrow |c| = \sqrt {10}

Note: If instead of the circle x2+y2−2x−4y+1=0{x^2} + {y^2} - 2x - 4y + 1 = 0 the equation of a circle is of the form x2+y2=r2{x^2} + {y^2} = {r^2}then directly we get center and radius. Distance is always positive, therefore if you get a negative value even though you have to consider positive value. Since radius can be framed as r=d2r = \dfrac{d}{2} where d is the overall diameter.