Question

Angle between an equipotential surface and electric lines of force is:
A. $0{}^\circ$
B. $90{}^\circ$
C. $180{}^\circ$
D. $270{}^\circ$

Answer 1

As a first step, you could recall that the surfaces that have the same potential throughout are known as equipotential surfaces. Now you could make a diagram of an equipotential surface by considering some electric field that makes an angle $\theta$ with the surface. Now you may express potential as the dot product of E and $dr$ and thus get the answer.
Formula used:
Potential,
$dV=E.dr$

Complete step-by-step solution:
In the question, we are asked to find the angle between an equipotential surface and electric lines of force. By electric lines of force, they mean the electric field on the equipotential surface.
In order to answer this question, let us consider an equipotential surface with an electric field directed at some angle $\theta$ (which we are supposed to find) with the surface.

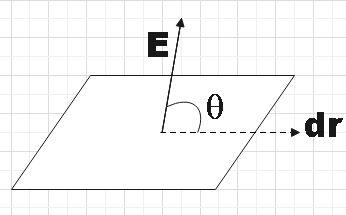
Therefore, we see that the angle made by E with $dr$ is $\theta$. Where, $dr$ is a vector along the equipotential surface. Now let us recall the expression for potential $dV$ in terms of E and $dr$.
$dV=E.dr$
$\Rightarrow dV=Edr\cos \theta$ ………………………………………… (1)
But we know that on an equipotential surface, the potential would be a constant throughout the surface. So, we get that,
For an equipotential surface,
$dV=0$
Now from (1) we have,
$dV=E.dr=0$
$\Rightarrow dV=Edr\cos \theta =0$
But we know that electric fields E and $dr$ cannot be zero. So, it would be the cosine of the angle between them that is zero. Therefore,
$\cos \theta =0$
$\therefore \theta ={{\cos }^{-1}}0=90{}^\circ$
Therefore, we found the angle between an equipotential surface and electric lines of force to be $90{}^\circ$. Hence, option B is the correct answer.

Note: It is one of the defined properties of the equipotential surface to have the electric field perpendicular to its surface. Some of the other properties are: (1) No two equipotential surfaces intersect. (2) Point charges have concentric spherical shells as their equipotential surfaces.