Question
Question: Angle between a pair of tangents drawn at the end points of the chord y + St = tx + 2 of curve C ∀t∈...
Angle between a pair of tangents drawn at the end points of the chord y + St = tx + 2 of curve C ∀t∈R, is
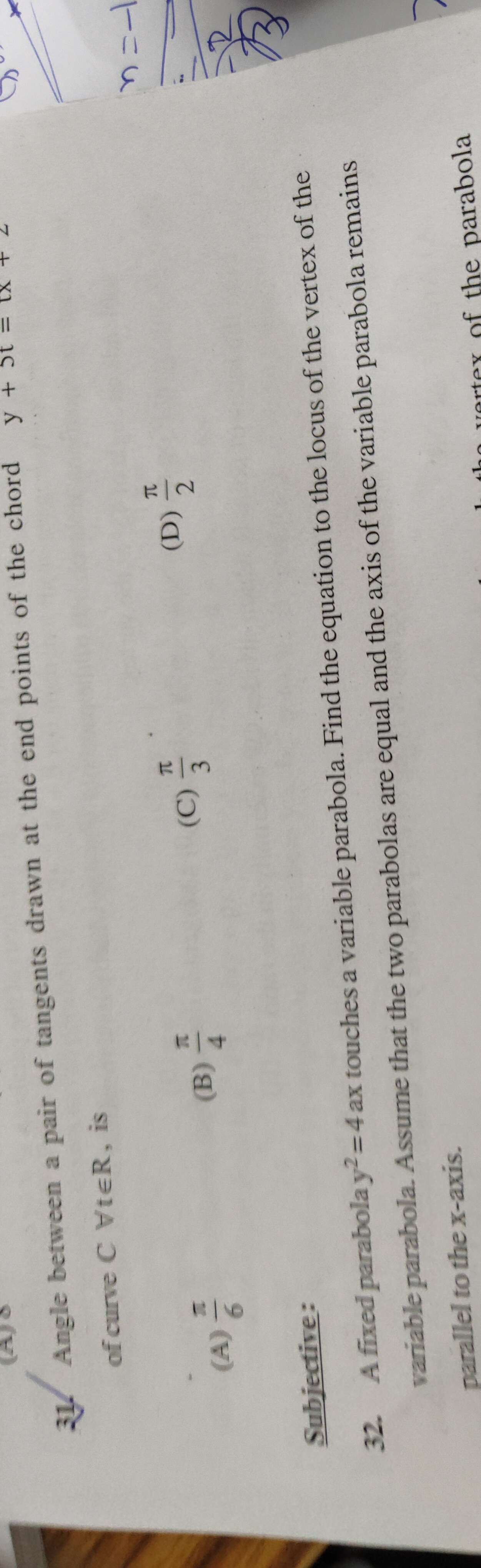
6π
4π
3π
2π
2π
Solution
The equation of the chord is given as y+St=tx+2. Rearranging this, we get y=tx+(2−St). If we interpret this as a family of tangents to the parabola y2=4ax, then for a tangent y=mx+c, the condition is c=a/m. Here, m=t and c=2−St. Therefore, 2−St=a/t, which implies St2−2t+a=0. Let t1 and t2 be the roots of this quadratic equation, representing the slopes of the tangents. The angle θ between the tangents is given by tanθ=1+t1t2t1−t2. From Vieta's formulas, t1t2=a/S. For the angle to be constant and independent of t, we consider the case where the tangents are perpendicular, i.e., 1+t1t2=0. This gives 1+a/S=0, or aS=−1. In this case, tanθ is undefined, implying θ=2π. The discriminant of St2−2t+a=0 is 4−4aS. If aS=−1, the discriminant is 4−4(−1)=8>0, ensuring two distinct real roots for t. Thus, the angle between the tangents is 2π.
