Question
Question: Find the sum of the series: $\frac{1}{2}+\frac{1}{8}+\frac{1}{24}+\frac{1}{64}+......+\frac{1}{k.2^{...
Find the sum of the series: 21+81+241+641+......+k.2k1+......
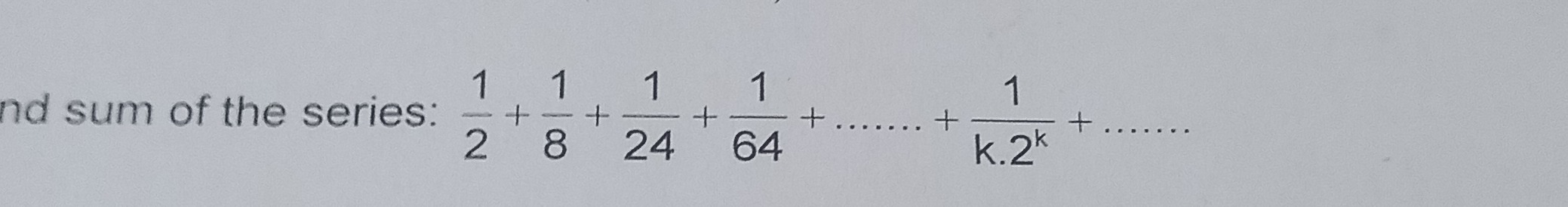
ln 2
Solution
The given series is S=21+81+241+641+.......
The general term of the series can be identified as Tk=k⋅2k1.
So, the series can be written in summation form as:
S=∑k=1∞k⋅2k1
We can rewrite this as:
S=∑k=1∞k(1/2)k
Recall the Maclaurin series expansion for ln(1−x):
The Maclaurin series for ln(1−x) is given by:
ln(1−x)=−x−2x2−3x3−4x4−…
This can be expressed in summation notation as:
ln(1−x)=−∑k=1∞kxk
This expansion is valid for ∣x∣<1.
Comparing our series S=∑k=1∞k(1/2)k with the general form −ln(1−x)=∑k=1∞kxk, we can see that x=21.
Since ∣x∣=∣1/2∣=1/2, which is less than 1, the expansion is valid.
Substitute x=1/2 into the formula for ln(1−x):
∑k=1∞k(1/2)k=−ln(1−21)
S=−ln(21)
Using the logarithm property ln(a/b)=lna−lnb and ln(1)=0:
S=−(ln1−ln2)
S=−(0−ln2)
S=ln2
The sum of the series is ln2.
