Solveeit Logo
Login

Question

Question: An urn contains \(m\) white and \(n\) black balls. Balls are drawn one by one till all the balls are...

An urn contains mm white and nn black balls. Balls are drawn one by one till all the balls are drawn. Probability that the second drawn ball is white is
(a) mm+n\dfrac{m}{m+n}
(b) m(n−1)(m+n)(m+n−1)\dfrac{m\left( n-1 \right)}{\left( m+n \right)\left( m+n-1 \right)}
(c) m(m−1)(m+n)(m+n−1)\dfrac{m\left( m-1 \right)}{\left( m+n \right)\left( m+n-1 \right)}
(d) mn(m+n)(m+n−1)\dfrac{mn}{\left( m+n \right)\left( m+n-1 \right)}

Explanation

Solution

The first ball that is chosen can be either white or black. We will find the probability of the first ball being white, then we will find the probability of the first ball being back. Then we will consider the event to be drawing the second ball, which is white. We will find the probability for this event. Then the final probability will take into account the probability that the first ball and second ball is white, and the probability that the first ball is black and the second ball is white.

Complete step by step answer:
Let us draw a diagram to understand the events.

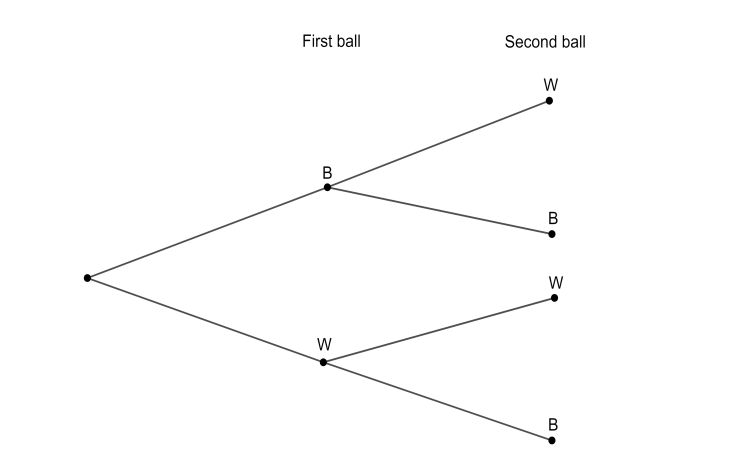
Now, the probability that the first ball is white is mm+n\dfrac{m}{m+n}, since there are mm white balls and m+nm+n total balls in the urn. Similarly, the probability that the first ball is black is nm+n\dfrac{n}{m+n}, as there are nn white balls and m+nm+n total balls.

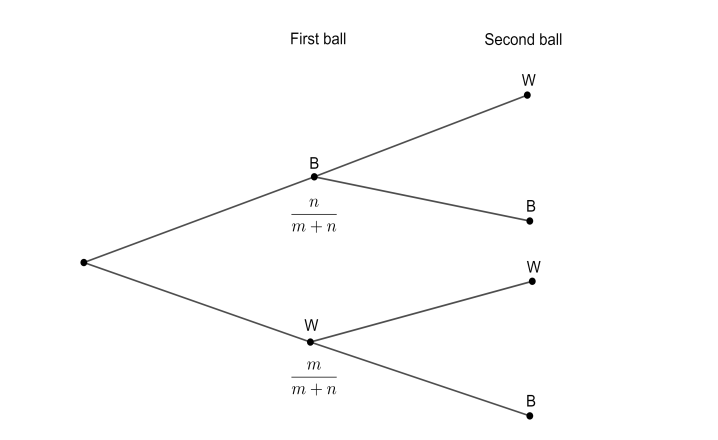
Next we will come to the second ball. The total number of balls left in the urn after drawing the first ball is m+n−1m+n-1. Let us fix the first ball to be black. Now, the probability that the second ball is white is P(BW)=nm+n×mm+n−1P\left( BW \right)=\dfrac{n}{m+n}\times \dfrac{m}{m+n-1}. The probability that the second ball is black is P(BB)=nm+n×n−1m+n−1P\left( BB \right)=\dfrac{n}{m+n}\times \dfrac{n-1}{m+n-1}.
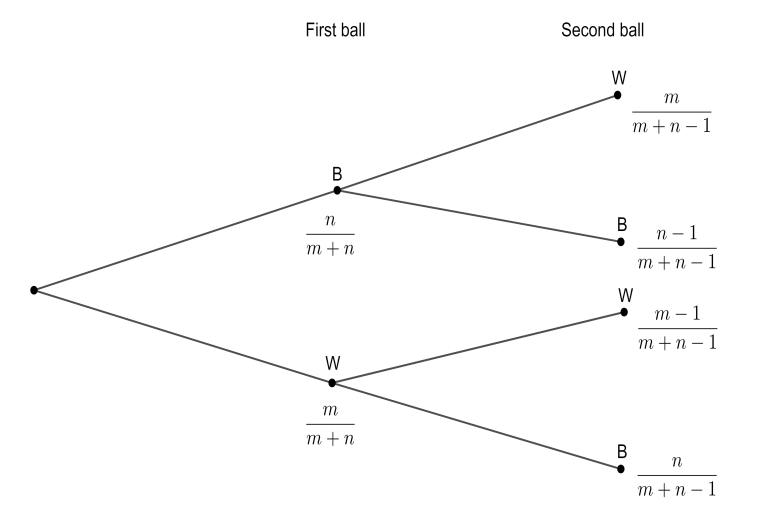
Now we will fix the first ball to be white. So, the probability that the second ball is white is P(WW)=mm+n×m−1m+n−1P\left( WW \right)=\dfrac{m}{m+n}\times \dfrac{m-1}{m+n-1}. And the probability that the second ball is black is P(WB)=mm+n×nm+n−1P\left( WB \right)=\dfrac{m}{m+n}\times \dfrac{n}{m+n-1}.

So, the probability that the second ball is white will be,
P=P(BW)+P(WW)P=P(BW)+P(WW)
Substituting the values of P(BW)P(BW) and P(WW)P(WW), we get
P=(nm+n×mm+n−1)+(mm+n×m−1m+n−1)P=\left( \dfrac{n}{m+n}\times \dfrac{m}{m+n-1} \right)+\left( \dfrac{m}{m+n}\times \dfrac{m-1}{m+n-1} \right)
Simplifying the above equation, we get the following
P=(mn+m(m−1)(m+n)(m+n−1)) =mn+m2−m(m+n)(m+n−1) =m(n+m−1)(m+n)(m+n−1) =mm+n\begin{aligned} & P=\left( \dfrac{mn+m\left( m-1 \right)}{\left( m+n \right)\left( m+n-1 \right)} \right) \\\ & =\dfrac{mn+{{m}^{2}}-m}{\left( m+n \right)\left( m+n-1 \right)} \\\ & =\dfrac{m\left( n+m-1 \right)}{\left( m+n \right)\left( m+n-1 \right)} \\\ & =\dfrac{m}{m+n} \end{aligned}
Hence, the probability that the second ball drawn is white is mm+n\dfrac{m}{m+n}.

So, the correct answer is “Option A”.

Note:
The key aspect of this question is multiplying the probability that the first ball is white or that it is black while calculating the probability that the second ball is white. Basically, we split the event of the second ball being white into two cases. Case 1 is BW, that is the first ball is black AND the second ball is white. Case 2 is WW, which means that the first ball is white AND the second ball is white.