Question

An RCL circuit has ${{f}_{1}}\text{ and }{{f}_{2}}$ as the half power frequency and ${{f}_{0}}$as the resonant frequency. The Q factor of the circuit is given by,
$\begin{aligned} & a)\dfrac{{{f}_{1}}+{{f}_{2}}}{2{{f}_{0}}} \\\ & b)\dfrac{{{f}_{1}}-{{f}_{0}}}{{{f}_{2}}-{{f}_{0}}} \\\ & c)\dfrac{{{f}_{0}}}{{{f}_{1}}-{{f}_{2}}} \\\ & d)\dfrac{{{f}_{1}}-{{f}_{2}}}{{{f}_{0}}} \\\ \end{aligned}$

Answer 1

The Q factor refers to the quality factor of the LCR circuit in series. It is given in the question that ${{f}_{1}}\text{ and }{{f}_{2}}$ are the half power frequencies and hence from this we can imply that it is a series LCR circuit. The quality factor LCR in series is defined as the ratio of power stored in the capacitor or the inductor of the at resonance to the average power absorbed by the resistance in the circuit. Hence we will express the Q factor of the circuit in terms of resonant frequency and half power frequencies using the above definition.

Complete step-by-step answer:

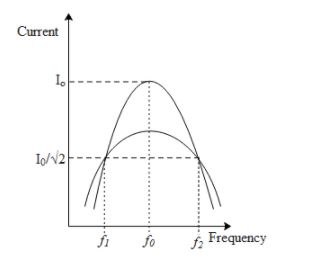
The above graph represents the variation of current in an LCR circuit with the increase in the frequency of the source. At resonance that is at ${{f}_{0}}$the current in the circuit is maximum. The half power dissipated across the circuit is given as,
$P=\dfrac{{{i}^{2}}Z}{2}$, where Z is the net impedance in the circuit and I is the circuit current. During the half power the impedance in the circuit does not change but current does. Hence the above equation can be written as, $P={{\left( \dfrac{i}{\sqrt{2}} \right)}^{2}}Z$. The value of the current during the half power frequency hence is given as $\dfrac{i}{\sqrt{2}}$.
As per the definition of Quality factor, It can be mathematically represented as,
$\begin{aligned} & Q=\dfrac{{{i}^{2}}{{X}_{L}}}{{{i}^{2}}R},where{{X}_{L}}(\text{Impedance due to inductor})=2\pi fL\text{L is the value of inductance and }\\!\\!'\\!\\!\text{ f }\\!\\!'\\!\\!\text{ is the } \\\ & \text{ }\\!\\!'\\!\\!\text{ f }\\!\\!'\\!\\!\text{ is the frequency of current in the circuit since the inductor and the resistor are connected in series, } \\\ & \text{the current }\\!\\!'\\!\\!\text{ i }\\!\\!'\\!\\!\text{ is the same} \\\ & Q=\dfrac{{{X}_{L}}}{R} \\\ \end{aligned}$
The bandwidth of the LCR circuit i.e.${{f}_{1}}-{{f}_{2}}$ is numerically equal to,
$\begin{aligned} & B.W={{f}_{1}}-{{f}_{2}}=\dfrac{R}{2\pi L}\text{Multiplying and dividing by }{{\text{f}}_{\text{0}}}\text{,we get} \\\ & {{f}_{1}}-{{f}_{2}}=\dfrac{R{{f}_{0}}}{2\pi L{{f}_{0}}}=\dfrac{{{f}_{0}}}{{}^{2\pi L{{f}_{0}}}/{}_{R}}=\dfrac{{{f}_{0}}}{{}^{{{X}_{L}}}/{}_{R}}\text{, since }Q=\dfrac{{{X}_{L}}}{R}, \\\ & {{f}_{1}}-{{f}_{2}}=\dfrac{{{f}_{0}}}{Q} \\\ & Q=\dfrac{{{f}_{0}}}{{{f}_{1}}-{{f}_{2}}} \\\ \end{aligned}$

So, the correct answer is “Option C”.

Note: It is to be noted that the quality factor for a LCR parallel circuit is given by, $Q=\dfrac{{{f}_{1}}-{{f}_{2}}}{{{f}_{0}}}$. In LCR series circuits at resonance the current is maximum. But in LCR parallel circuits the current through the circuit is minimal.