Question

An oscillator of mass $M$ is at rest in its equilibrium position in a potential $V = \dfrac{1}{2}k{\left( {x - X} \right)^2}$ . A particle of mass $m$ comes from the right with speed $u$ and collides completely inelastically with $M$ and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. Find the amplitude of the oscillation after 13 collisions. ( $M = 10$ , $m = 5$ , $u = 1$ , $k = 1$ ).
A) $\dfrac{1}{{\sqrt 3 }}$
B) $\dfrac{1}{2}$
C) $\dfrac{2}{3}$
D) $\sqrt {\dfrac{3}{5}}$

Answer 1

The oscillator consists of a mass attached to a spring fixed at one end. The linear momentum of the system before and after the collision will remain constant. The mass of the system after a collision will be the sum of the oscillator and that of the particle attached to it. Each time the oscillator crosses its equilibrium position, a particle will get stuck to it after colliding with it. The kinetic energy of the system after the 13 collisions and the kinetic energy of the spring attached to the oscillator will be equal.

Formulas used:
-The kinetic energy of a spring is given by, $KE = \dfrac{1}{2}k{A^2}$ where $k$ is the spring constant and $A$ is its amplitude.
-The kinetic energy of a body is given by, $KE = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the body and $v$ is its velocity.
-The linear momentum of a body is given by, $p = mv$ where $m$ is the mass of the body and $v$ is its velocity.

Complete step by step answer.
Step 1: Sketch a figure describing the system under consideration and list its given parameters.
The below figure depicts the system under consideration before collision.

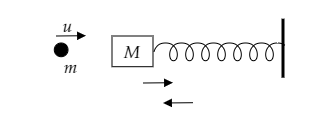
The mass of the oscillator is given to be $M = 10$ .
The mass and speed of the colliding particle are given to be $m = 5$ and $u = 1$ .
Initial the velocity of the oscillator is zero.
The spring constant of the spring is given to be $k = 1$ .
Step 2: Apply the conservation of linear momentum before and after the first collision.
Let ${v_1}$ be the velocity of the system (oscillator and particle) after the first collision.
The linear momentum of the system before collision will be $mu + M \times 0 = mu$ .
The linear momentum of the system after collision will be $\left( {M + 1m} \right){v_1}$ .
The conservation of linear momentum states that the linear momentum of the system before collision will be equal to its linear momentum after collision.
Thus we have $mu = \left( {M + 1m} \right){v_1}$
$\Rightarrow {v_1} = \dfrac{{mu}}{{M + 1m}}$
Similarly, the velocity of the system after 13 collisions will be ${v_{13}} = \dfrac{{mu}}{{M + 13m}}$ ------ (1)
Substituting for $M = 10$ , $m = 5$ and $u = 1$ in equation (1) we get, ${v_{13}} = \dfrac{{5 \times 1}}{{10 + \left( {13 \times 5} \right)}} = \dfrac{5}{{75}} = \dfrac{1}{{15}}$
Thus the velocity of the system after 13 collisions is obtained as ${v_{13}} = \dfrac{1}{{15}}$ .
Step 3: Express the kinetic energy of the system and that of the spring after 13 collisions.
The kinetic energy of the system after 13 collisions can be expressed as
$K{E_{system}} = \dfrac{1}{2}\left( {M + 13m} \right){v_{13}}^2$ -------- (2)
Substituting for $M = 10$ , $m = 5$ and ${v_{13}} = \dfrac{1}{{15}}$ in equation (2) we get, $K{E_{system}} = \dfrac{1}{2}\left[ {10 + \left( {13 \times 5} \right)} \right]{\left( {\dfrac{1}{{15}}} \right)^2} = \dfrac{1}{6}$
Thus the kinetic energy of the system is obtained as $K{E_{system}} = \dfrac{1}{6}$ .
Now the kinetic energy of the spring is expressed as $K{E_{spring}} = \dfrac{1}{2}k{A^2}$ ---------- (3)
Substituting for $k = 1$ in equation (3) we get, $K{E_{spring}} = \dfrac{1}{2} \times 1 \times {A^2} = \dfrac{{{A^2}}}{2}$
Now the kinetic energy of the system and that of the spring after 13 collisions will be the same.
i.e., $K{E_{spring}} = K{E_{system}}$ -------- (4)
Substituting for $K{E_{system}} = \dfrac{1}{6}$ and $K{E_{spring}} = \dfrac{{{A^2}}}{2}$ in equation (4) we get, $\dfrac{{{A^2}}}{2} = \dfrac{1}{6}$
$\Rightarrow A = \sqrt {\dfrac{2}{6}} = \dfrac{1}{{\sqrt 3 }}$
Thus the amplitude of the spring is obtained as $A = \dfrac{1}{{\sqrt 3 }}$ .

So the correct option is A.

Note: After each collision, the colliding particle will get stuck to the oscillating mass. So the mass of the system after the second, third and so on collisions till the thirteenth collision will be $\left( {M + 2m} \right),\left( {M + 3m} \right),......\left( {M + 13m} \right)$ . In an inelastic collision, the linear momentum of the system will be conserved.