Question

An open U-tube contains mercury. When $11.2\,cm$ of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial unit?
A. $0.56\,cm$
B. $1.35\,cm$
C. $0.41\,cm$
D. $2.32\,cm$

Answer 1

We can solve this question, using the concept of height and pressure. The pressure on the outer surface of both the sides of the u tube will be atmospheric pressure. The pressure inside the tube at the same height will be equal. We will use Bernoulli’s equation to solve this problem.

Complete step by step answer:
We are given that the tube is in U shape and it contains mercury. Initially, the level of mercury at both the ends of the tube will be equal. When $11.2\,cm$ of water will be poured at one of the arms of the tube, there will be some pressure applied to the mercury at that arm. This pressure will push the mercury and thus the level of mercury in another arm will rise. Let’s draw a diagrammatic representation of the same:

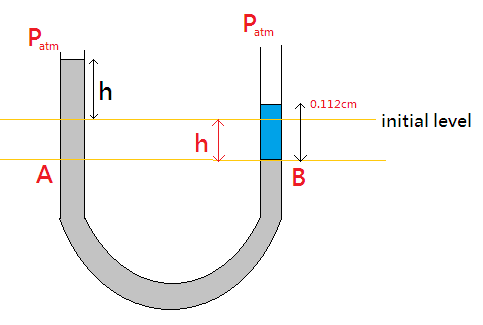
From the figure, we have:
The initial level of water is marked. When water is poured from the right arm, mercury in the left arm rises. The water from the initial level pushes the mercury up to point B.
As we know that pressure at any point is given as:
$P = {P_{ref}} + \rho gh$
Here $P$ is the pressure at the required point
${P_{ref}}$ is the reference pressure at that point initially
$\rho$ is the density of the liquid
$g$ is acceleration due to gravity
$h$ is the change in level of water.
Pressure at point B will with reference to atmospheric pressure will be:
${P_B} = {P_{atm}} + \rho gh$
Since the liquid at point C is water, therefore Substituting the value of $h = 11.2\,cm$ , we get
$\Rightarrow {P_B} = {P_{atm}} + {\rho _w}g(0.112)$ --equation $1$
Here ${\rho _w}$ indicates the density of water.
Similarly, the pressure at point A with reference to the atmospheric pressure at the top of left arm will be: The height at left arm above point A is $2h$ .
${P_A} = {P_{atm}} + \rho g(h + h)$
$\Rightarrow {P_A} = {P_{atm}} + {\rho _m}g(2h)$ --equation $2$
Here, ${\rho _w}$ is the density of mercury.
The pressure inside the same liquid at same height must be equal,
$\therefore {P_B} = {P_A}$
Substituting the values from equation $1,2$ we have
$\Rightarrow {P_{atm}} + {\rho _w}g(0.112) = {P_{atm}} + {\rho _m}g2h$
$\Rightarrow {\rho _w}(0.112) = {\rho _m}2h$
The density of water is ${\rho _w} = 1000kg\,{m^{ - 3}}$ and density of mercury is ${\rho _m} = 13600kg\,{m^{ - 3}}$ , substituting these values, we get
$h = \dfrac{{(1000)(0.112)}}{{2(13600)}}$
$\Rightarrow h = 0.00412\,m$
Thus, the mercury rise in the other arm from its initial unit is of $0.41\,cm$

So, the correct answer is “Option C”.

Note:
Pressure is the ratio of force per unit area and it is used to calculate the air pressure of a column of known height against some other liquid.
The widely used units of measurement of height is inches of mercury and inches in case of water.
U tube manometers work on the same principle which is used to find the pressure.