Question

An open knife edge of mass m is dropped from a height h on a wooden floor. If the blade penetrates a distance d into the wood, then the average resistance offered by wood, to blade is?
A) $mg\left( {1 - \dfrac{h}{d}} \right)$
B) $mg$
C) $mg{\left( {1 + \dfrac{h}{d}} \right)^2}$
D) $mg\left( {1 + \dfrac{h}{d}} \right)$

Answer 1

We can solve this question by using the work energy theorem. When the knife starts to fall from height h then it starts to gain velocity from zero until it reaches on the wooden floor and after reaching there it starts to penetrate floor and lose their kinetic energy and comes to rest at distance $d$.
We apply here the work energy theorem.

Complete step by step answer:
For better understanding we make the first diagram of this.
A knife initially at h height forms the surface of a wooden floor. At the surface we take point 1 where knives strike on the floor. And we mark another point 2 below it at distance d where the knife stops finally.

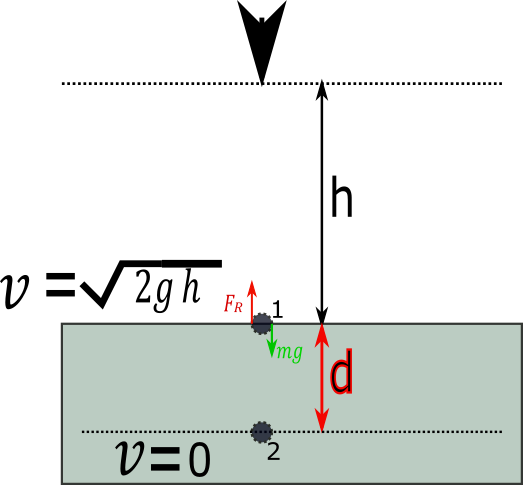
Step 1:
First we find the velocity of the knife when it reaches point 1 on the surface of the wooden floor.
Potential energy at h height = kinetic energy at lower point.
$\Rightarrow mgh = \dfrac{1}{2}m{v^2}$
Solving it
$\Rightarrow {v^2} = \sqrt {2gh}$ ................. (1)
This is the velocity of a knife when it reaches the surface of the floor.
Step 2:
Now we apply work energy theorem between point 1 and point 2
Work energy theorem states that the work done by all forces is equal to the change in kinetic energy.
work done by all forces=change in K.E
At point 1
Velocity of knife is $\Rightarrow {v^2} = \sqrt {2gh}$
There are two Force acts on knives when it is at point 1.
- Weight of knife $mg$ downward
- by Resistance offered wood ${F_R}$ upward direction
At point 2 Velocity of knife becomes 0
So apply work energy theorem between point and point 2
Work done by mg = $mgd$
Work done by ${F_R}$ is $- {F_R}d$ negative sign due to direction of force is opposite to displacement $d$
work done by all forces=change in K.E
$\Rightarrow mgd - {F_R}d = {K_2} - {K_1}$
${K_2} = \dfrac{1}{2}m{(0)^2}$ And ${K_1} = \dfrac{1}{2}m{v^2}$
Put these value
$\Rightarrow mgd - {F_R}d = \dfrac{1}{2}m{(0)^2} - \dfrac{1}{2}m{v^2}$
Further solving and put the value of $v = \sqrt {2gh}$ from equation (1)
$\Rightarrow {F_R}d = mgd + \dfrac{1}{2}m{\left( {\sqrt {2gh} } \right)^2}$
$\Rightarrow {F_R}d = mgd + mgh$
Solving again
$\Rightarrow {F_R}d = mg\left( {d + h} \right)$
$\Rightarrow {F_R} = mg\left( {\dfrac{{d + h}}{d}} \right)$
So this is the by Resistance offered wood ${F_R}$ can be written as
$\therefore {F_R} = mg\left( {1 + \dfrac{h}{d}} \right)$

Hence option D is correct.

Note:
We can solve these types of questions in these simple steps. We can also solve by some other method but applying work energy theorem makes it easy. We can also apply the work energy theorem for higher point means initial and final condition of the knife. Initially the knife has zero velocity and finally also has zero velocity.
Means change in K.E is zero must equal to work done by all force to take knife from height $h$ to $d$ depth,
$\Rightarrow mg\left( {h + d} \right) - {F_R}d = 0 \\\ \Rightarrow {F_R} = mg\left( {\dfrac{{h + d}}{d}} \right) \\\ \Rightarrow {F_R} = mg\left( {1 + \dfrac{h}{d}} \right) \\\$