Question

An open cylindrical tank whose base is a circle is to be constructed of metal sheet so as to contain a volume of $\pi {{a}^{3}}cu.cm$ of water. Find the dimensions so that the quantity of the metal sheet required is minimum.

Answer 1

In the given question, we are given the volume of an open cylinder and we have to find the dimensions of the container such that the quantity of the metal sheet required is minimum. We will first assume that the radius of the cylindrical tank is $r$ cm and the height of the cylindrical tank is $h$ cm. Using the given value of the volume of the tank, we will find an expression, which is, $h=\dfrac{{{a}^{3}}}{{{r}^{2}}}$. Then, we will find the surface area of the tank and then we will find the first and second derivative with respect to the radius. Then, we will use another expression, $a=r$. From the two expressions we have obtained, we will get the dimensions such that the quantity of the metal sheet required is minimum.

Complete step by step answer:
According to the given question, we are given the volume of the cylindrical tank and we have to find the dimensions of the tank such that the quantity of the metal sheet required is minimum.
Let the $r$ be the radius of the cylindrical tank and $h$ be the height if the cylindrical tank, then the volume is represented as $V$ and the surface area of the tank be represented as $S$.

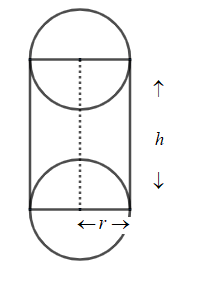
Volume of the tank $=\pi {{a}^{3}}$
$\Rightarrow \pi {{r}^{2}}h=\pi {{a}^{3}}$
$\Rightarrow {{r}^{2}}h={{a}^{3}}$
Writing the above expression in terms of ‘h’ we get,
$\Rightarrow h=\dfrac{{{a}^{3}}}{{{r}^{2}}}$
Now, we will write the surface area of the cylindrical tank which we have to cover using the metal sheet. We have,
$S=2\pi rh+\pi {{r}^{2}}$
Substituting the value of ‘h’ in the above expression, we will get,
$\Rightarrow S=2\pi r\left( \dfrac{{{a}^{3}}}{{{r}^{2}}} \right)+\pi {{r}^{2}}$
Cancelling the common terms, we will get,
$\Rightarrow S=2\pi \dfrac{{{a}^{3}}}{r}+\pi {{r}^{2}}$
Now, we will find the first derivative of the above expression, we will get,
$\dfrac{dS}{dr}=2\pi {{a}^{3}}\left( -1 \right){{r}^{-2}}+2\pi r$
$\Rightarrow \dfrac{dS}{dr}=-2\pi {{a}^{3}}{{r}^{-2}}+2\pi r$
Putting $\dfrac{dS}{dr}=0$, we get,
$-2\pi {{a}^{3}}{{r}^{-2}}+2\pi r=0$
Rearranging the expression, we have,
$\Rightarrow 2\pi {{a}^{3}}{{r}^{-2}}=2\pi r$
Cancelling out the common terms across the equality, we have,
$\Rightarrow {{a}^{3}}{{r}^{-2}}=r$
$\Rightarrow {{a}^{3}}={{r}^{3}}$
Taking the cube root on either side, we get,
$\Rightarrow a=r$-----(1)
Now, we will find the second derivative of the surface area expression, we will get,
$\dfrac{d}{dr}\left( \dfrac{dS}{dr} \right)=\dfrac{d}{dr}\left( -2\pi {{a}^{3}}{{r}^{-2}}+2\pi r \right)$
Differentiating the expression further, we get,
$\Rightarrow \dfrac{{{d}^{2}}S}{d{{r}^{2}}}=-2\pi {{a}^{3}}(-2){{r}^{-3}}+2\pi$
$\Rightarrow \dfrac{{{d}^{2}}S}{d{{r}^{2}}}=4\pi {{a}^{3}}{{r}^{-3}}+2\pi$
From equation (1), we will substitute the value of $a=r$ in the second derivative we got, we have,
${{\left( \dfrac{{{d}^{2}}S}{d{{r}^{2}}} \right)}_{a=r}}=4\pi {{a}^{3}}\left( {{a}^{-3}} \right)+2\pi$
$\Rightarrow {{\left( \dfrac{{{d}^{2}}S}{d{{r}^{2}}} \right)}_{a=r}}=4\pi +2\pi =6\pi >0$
Since, the second derivative gives a value greater than 0, so we will have the minimum surface area when $a=r$.
That is,
$h=\dfrac{{{a}^{3}}}{{{r}^{2}}}$ can be written as,
$\Rightarrow h=\dfrac{{{r}^{3}}}{{{r}^{2}}}=r$
$\Rightarrow h=r$
Therefore, when $h=r$ then the quantity of metal sheet required to cover the tank is minimum.

Note: The formula of the volume of the cylinder should be written correctly. In the above solution, the formula of the surface area had only one $\pi {{r}^{2}}$, this is because the tank is open and due to which the upper part is excluded and only the bottom part is taken under consideration. There is a possibility of using the usual formula of the surface area of a cylinder. So as per the question, the formula also has to be modified.