Question

An open box with a square base is to be made out of a given quantity of cardboard of area ${{c}^{2}}$square units. Show that the maximum volume of the box is $\dfrac{{{c}^{3}}}{6\sqrt{3}}$ cubic units?

Answer 1

We start solving the problem by assigning variables to the length of the side of the base and height of the base. We then find the surface area of the box which will be equal to the area of card board. We this to find the volume of the box. Since we need the maximum volume of boxes, we differentiate the volume and equate it to 0 to get the required value. We check the condition of maximum and substitute in the volume of the box to get the maximum volume.

Complete step-by-step solution:
According to the problem, we have an open box with a square base is to be made out of a quantity of cardboard of area ${{c}^{2}}$square units. We need to prove that the maximum volume of the box is $\dfrac{{{c}^{3}}}{6\sqrt{3}}$ cubic units.
Let us assume the side of the base be ‘a’ units and the height of the box be ‘h’ units as shown in the figure below.

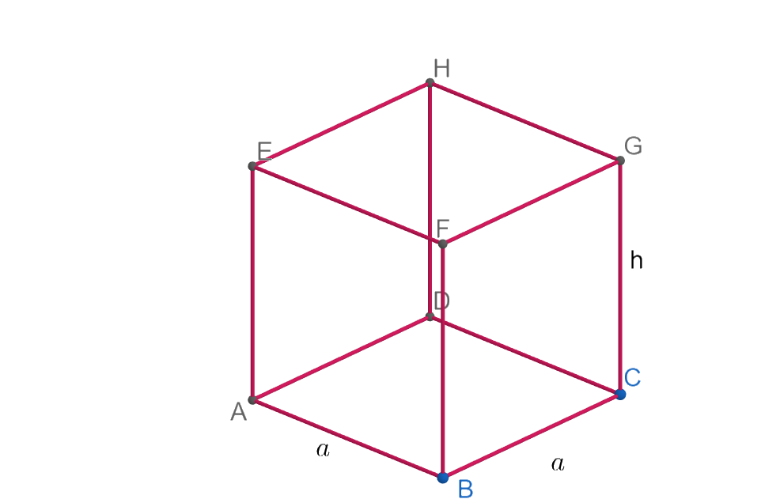
From the figure, we can see that the total area of the cardboard is equal to the sum of the area of the base and surface area of the other 4 sides.
i.e., Area of cardboard = Area of ABCD + Area of ABFE + Area of BCGF + Area of CDGH + Area of DAFH -----(1). (since the given box is open on top, the area of EFGH is not considered).
From the figure, we can see faces other than the base are rectangle with length ‘a’ and breadth ‘h’.
We know that the area of a square with side ‘a’ is ${{a}^{2}}$ sq. units. The area of the rectangle length ‘l’ and breadth ‘b’ is $lb$ sq. units. We use this in equation (1).
$\Rightarrow {{c}^{2}}={{a}^{2}}+\left( a\times h \right)+\left( a\times h \right)+\left( a\times h \right)+\left( a\times h \right)$.
$\Rightarrow {{c}^{2}}={{a}^{2}}+ah+ah+ah+ah$.
$\Rightarrow {{c}^{2}}={{a}^{2}}+4ah$.
$\Rightarrow {{c}^{2}}-{{a}^{2}}=4ah$.
$\Rightarrow h=\dfrac{{{c}^{2}}-{{a}^{2}}}{4a}$ ------(2).
We know that the volume of the box with base area ‘a’ and height ‘h’ is $V={{a}^{2}}h$ cubic units.
From equation (2), we get $V={{a}^{2}}\left( \dfrac{{{c}^{2}}-{{a}^{2}}}{4a} \right)$.
$\Rightarrow V=\left( \dfrac{a{{c}^{2}}-{{a}^{3}}}{4} \right)$ cubic units.
But we need the maximum volume of the box. Here c is already given in the problem so, the only unknown present here is a.
Let us differentiate with respect to a.
$\Rightarrow \dfrac{d}{da}\left( V \right)=\dfrac{d}{da}\left( \dfrac{a{{c}^{2}}-{{a}^{3}}}{4} \right)$.
We know that $\dfrac{d}{dx}\left( f\left( x \right)+g\left( x \right) \right)=\dfrac{d}{dx}\left( f\left( x \right) \right)+\dfrac{d}{dx}\left( g\left( x \right) \right)$.
$\Rightarrow \dfrac{dV}{da}=\dfrac{d}{da}\left( \dfrac{a{{c}^{2}}}{4} \right)-\dfrac{d}{da}\left( \dfrac{{{a}^{3}}}{4} \right)$.
$\Rightarrow \dfrac{dV}{da}=\dfrac{{{c}^{2}}}{4}\dfrac{d}{da}\left( a \right)-\dfrac{d}{da}\left( \dfrac{{{a}^{3}}}{4} \right)$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$.
$\Rightarrow \dfrac{dV}{da}=\dfrac{{{c}^{2}}}{4}\times 1-\dfrac{3{{a}^{2}}}{4}$.
$\Rightarrow \dfrac{dV}{da}=\dfrac{{{c}^{2}}-3{{a}^{2}}}{4}$ ------(3).
Now, we find the value of a in terms of c by equating $\dfrac{dV}{da}$ to 0 i.e., $\dfrac{dV}{da}=0$.
$\Rightarrow \dfrac{{{c}^{2}}-3{{a}^{2}}}{4}=0$.
$\Rightarrow {{c}^{2}}-3{{a}^{2}}=0$.
$\Rightarrow 3{{a}^{2}}={{c}^{2}}$.
$\Rightarrow {{a}^{2}}=\dfrac{{{c}^{2}}}{3}$.
$\Rightarrow a=\dfrac{c}{\sqrt{3}}$ -------(4).
Let us differentiate equation (3) with respect to a.
$\Rightarrow \dfrac{{{d}^{2}}V}{d{{a}^{2}}}=\dfrac{d}{da}\left( \dfrac{{{c}^{2}}-3{{a}^{2}}}{4} \right)$.
$\Rightarrow \dfrac{{{d}^{2}}V}{d{{a}^{2}}}=\dfrac{d}{da}\left( \dfrac{{{c}^{2}}}{4} \right)-\dfrac{d}{da}\left( \dfrac{3{{a}^{2}}}{4} \right)$.
We know that $\dfrac{d}{dx}\left( a \right)=0$.
$\Rightarrow \dfrac{{{d}^{2}}V}{d{{a}^{2}}}=-\dfrac{6a}{4}$. Let us substitute equation (3) here.
$\Rightarrow \dfrac{{{d}^{2}}V}{d{{a}^{2}}}=-\dfrac{6\left( \dfrac{c}{\sqrt{3}} \right)}{4}$.
$\Rightarrow \dfrac{{{d}^{2}}V}{d{{a}^{2}}}=-\dfrac{\sqrt{3}\left( c \right)}{2}<0$. So, we have maximum volume at $a=\dfrac{c}{\sqrt{3}}$.
Now, we substitute $a=\dfrac{c}{\sqrt{3}}$ in finding the volume of the box.
$\Rightarrow V=\left( \dfrac{\left( \dfrac{c}{\sqrt{3}} \right){{c}^{2}}-{{\left( \dfrac{c}{\sqrt{3}} \right)}^{3}}}{4} \right)$.
$\Rightarrow V=\left( \dfrac{\left( \dfrac{{{c}^{3}}}{\sqrt{3}} \right)-\left( \dfrac{{{c}^{3}}}{3\sqrt{3}} \right)}{4} \right)$.
$\Rightarrow V=\left( \dfrac{\left( \dfrac{3{{c}^{3}}-{{c}^{3}}}{3\sqrt{3}} \right)}{4} \right)$.
$\Rightarrow V=\dfrac{2{{c}^{3}}}{12\sqrt{3}}$.
$\Rightarrow V=\dfrac{{{c}^{3}}}{6\sqrt{3}}$ cubic units.
$\therefore$ we have proved the maximum volume of the box as $\dfrac{{{c}^{3}}}{6\sqrt{3}}$ cubic units.

Note: We should not take c as a constant as it is already mentioned in the problem which leads it to a constant. Whenever we get this type of problem, we need to start by assigning the variables to the unknowns which lead us to the solution. We should make calculation mistakes and have confusion in the formulas of differentiation while solving this problem. Similarly, we can expect the problem to find the maximum volume if the top of the box is closed.