Question
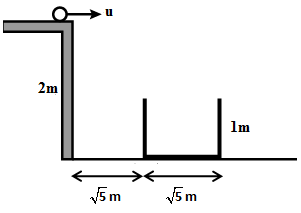
Question: An open box of height 1 m is placed near a 2 m high table as shown. Marbles roll on the table and ar...
An open box of height 1 m is placed near a 2 m high table as shown. Marbles roll on the table and are collected in the box. umax and umin are the maximum and minimum values of velocity of marbles to fall into the box. Find the value of umax−umin (in m/s).
Solution
The vertical component of the initial velocity of marble is zero. We can use a kinematic equation in vertical direction to determine the time taken by the marble to fall in the box. Then we can use the kinematic equation in the horizontal direction to determine the initial velocity for both the cases.
Formula used:
s=ut+21at2
Here, s is the distance, u is the initial velocity, a is the acceleration and t is the time.
Complete step by step answer:
We need to find the time required for the marbles to fall into the box. If we use the kinematic equation in the vertical direction, we can find the time as follows,
sy=uyt+21gt2
Here, sy is the vertical distance covered by the marble which is 1 m, uy is the vertical component of initial velocity, g is the acceleration due to gravity and t is the time.
We can observe here that the marbles were sliding horizontally on the table. Therefore, their initial velocity has only horizontal component and vertical component is zero.
We substitute 1 m for sy, 0 for uy and 10m/s2 for g in the above equation.
1=(0)t+21(10)t2
⇒t2=51
⇒t=51
The time to fall into the box will be the same for both the cases.
We now, use the kinematic equation in horizontal direction as follows,
sx=uxt …… (1)
We see in the above equation, the term of acceleration due to gravity is absent since the acceleration due to gravity does not affect the horizontal motion of the object.For minimum initial velocity, we substitute 5m for sx and 51 for t in the above equation.
5=umin(51)
⇒umin=55
⇒umin=5m/s
For maximum initial velocity, we substitute (5+5)m for sx and 51 for t in equation (1) equation.
5+5=umax(51)
⇒(4.472)5=umax
⇒umax=10m/s
Now, we have to determine the value of umax−umin, therefore,
umax−umin=10−5
∴umax−umin=5m/s
Therefore, the value of umax−umin is 5 m/s.
Note: Students should always take the sign of acceleration due to gravity as positive for the downward motion of the body and for the upward motion, take acceleration due to gravity as negative. For the horizontal motion of the body, we can directly use the relation s=ut, where, s is distance, u is the initial velocity and t is the time. Students should
understand which kinematic equation should be used for different kinds of questions. For this question we don’t know the final velocity of the marble. Therefore, we have taken the kinematic equation which does not have the term final velocity.
