Question

An open box is to be made out of a piece of paper of cardboard measuring (24cm × 24cm) by cutting off equal squares from the corners and turning up the sides. Find the height of the box when it has maximum volume.
A. 4
B. 10
C. 15
D. 20

Answer 1

In order to solve this problem we need to assume the variable x as the length of the box is cut from the two corners of the one side of the square paper. Then we need to calculate the volume of the open box in terms of x. Differentiating the volume and equating it to zero we will be getting the value of x which is denoting the point of maxima or minima after checking its maxima or minima and putting the maxima point in the volume we will get the right answer.

Complete step by step answer:
The figure for this problem can be drawn as,

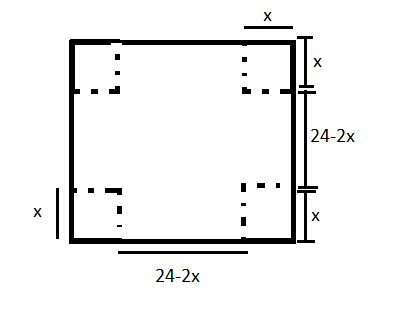
The length x is cut from every corner of the paper so that we can fold it and it looks like an open box. It means the height of the box is x cm.
Then the volume of the box will be ${\left( {24 - 2x} \right)^2}x$.
On solving it further we get the volume V as:
$V = {\left( {24 - 2x} \right)^2}x$
On differentiating the above volume with respect to x we get,
$\dfrac{{dV}}{{dx}} = \dfrac{{d{{\left( {24 - 2x} \right)}^2}x}}{{dx}}$
We will use here uv rule to differentiate the term.
When we differentiate uv that is (uv)’ we get (uv)’ = u’v + uv’.

$$\dfrac{{dV}}{{dx}} = \dfrac{{d{{\left( {24 - 2x} \right)}^2}x}}{{dx}} = 2\left( { - 2} \right)\left( {24 - 2x} \right)x + {\left( {24 - 2x} \right)^2} \\\ \dfrac{{dV}}{{dx}} = \left( {24 - 2x} \right)\left( { - 4x + 24 - 2x} \right) = \left( {24 - 2x} \right)\left( {24 - 6x} \right) \\\$$

On equating it to zero to get the value of x,
$\dfrac{{dV}}{{dx}} = \left( {24 - 2x} \right)\left( {24 - 6x} \right) = 0$
We got the value of x = 12, 4.
The value of x as 12 will be neglected because it will not be a box if we cut the length of 12cm from both the sides.
So, the value of x is 4cm.
And the maximum volume of box will be $\Rightarrow {\left( {24 - 2\left( 4 \right)} \right)^2}\left( 4 \right) = 1024c{m^3}$
We need to find the height when the volume is maximum. If we observe the figure we can clearly see that x is the height itself and it is 4cm.
If we want to check that the maximum volume will be at 4 or not we will double differentiate the volume at 4 and if it is negative it means this point is point of maxima so, we do,
$\dfrac{{d\left( {\dfrac{{dV}}{{dx}}} \right)}}{{dx}} = \dfrac{{d\left( {\left( {24 - 2x} \right)\left( {24 - 6x} \right)} \right)}}{{dx}} \\\ \dfrac{{d\left( {\dfrac{{dV}}{{dx}}} \right)}}{{dx}} = \left( {24 - 2x} \right)\left( { - 6} \right) + \left( { - 2} \right)\left( {24 - 6x} \right) \\\$
On putting the value of x = 4 in the above equation we get,
$\dfrac{{d\left( {\dfrac{{dV}}{{dx}}} \right)}}{{dx}} = \left( {24 - 8} \right)\left( { - 6} \right) + \left( { - 2} \right)\left( {24 - 24} \right) = - 96$
Hence the value is negative so, point 4 is the point of maxima.

So, the correct answer is “Option A”.

Note: In such problems you need to calculate the term which you have to maximize or minimize in terms of a single variable and then differentiate once and equate the differentiation to zero then get the value of variable and then solve algebraically to get the value of variable. The value you got is the maxima or minima point where the function has its maximum value. You can check the value of maximum and minimum by double differentiating the term if it is negative on that point then that point is maxima if it is positive on that point then that point is minima. Knowing this will solve your problems and will give you the right answer.