Question

An opaque cylindrical tank with an open top has a diameter of 3.00m and is completely filled with water. When the setting sun reaches an angle of $37{}^\circ$ above the horizon, sunlight ceases to illuminate any part of the bottom of the tank. How deep is the tank?

Answer 1

You could first make a ray diagram and find the point at which the light might have fallen at bottom of the tank to result in no bottom part being illuminated. Now you could use Snell's law to find the distance the refracted ray travelled to reach the bottom. Finally Pythagorean theorem will get you the depth of the tank.

Formula used: Snell’s law,
${{\mu }_{a}}\sin i={{\mu }_{w}}\sin r$

Complete step by step answer:
In the question, we are given an opaque cylindrical tank that is open at the top and has a diameter of 3m filled completely with water. At $37{}^\circ$ above the horizon, the sunlight doesn’t illuminate any part of the bottom of the tank. We are supposed to find the depth of the tank in meters.

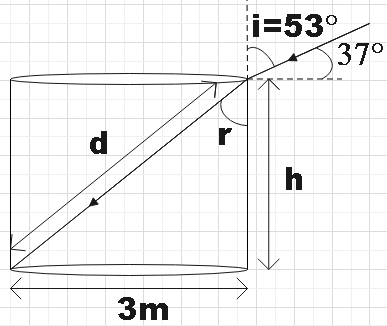
The refracted ray should have taken the path shown in the figure and that how no part of the bottom of the tank was illuminated. Also, we are given that the sunlight makes an angle $37{}^\circ$ with the horizon, so,
$37{}^\circ +i=90{}^\circ$
$\Rightarrow i=53{}^\circ$
Now, we are said that the tank is completely filled with water. So the sunlight is traveling from rarer (air) medium to denser (water) medium. We could recall Snell’s law given by,
${{\mu }_{a}}\sin i={{\mu }_{w}}\sin r$
$\Rightarrow 1\times \sin 53=\dfrac{4}{3}\sin r$
$\Rightarrow \sin r=\dfrac{3}{4}\times \dfrac{4}{5}$
$\Rightarrow \sin r=\dfrac{3}{5}=\dfrac{3}{d}$
$\therefore d=5m$
Now by using Pythagorean theorem we have,
${{3}^{2}}+{{h}^{2}}={{d}^{2}}$
$\Rightarrow h=\sqrt{25-9}$
$\therefore h=\pm 4$
Therefore, we found the depth of the tank to be 4m.

Note: It is pretty obvious that we have taken the positive value for depth as the measurement of length can’t be a negative value. We have also directly substituted the values for refractive indices of water and air as these values should be known to you. Also, in the ray diagram after refraction the ray moves closer to the normal as the light moves from rarer to denser medium.