Question
Question: An old record player of \[15.0cm\] radius turns at \[33.0\] rev min-1 while mounted on a \[30{}^\cir...
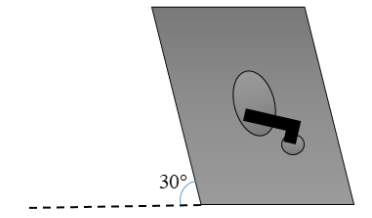
An old record player of 15.0cm radius turns at 33.0 rev min-1 while mounted on a 30∘ incline as shown in fig.
a) If a mass m can be placed anywhere on the rotating record, where is the most critical place on the disc where slipping might occur.
b) Calculate the least possible coefficient of friction that must exist if no slipping occurs.
Solution
As the Disc is moving on the record player so, there is a centrifugal force which acts outwards from the Center of disc. Also the frictional Force acts opposite to the motion of the record player.
Complete answer:
Given radius of record player 15.0 cm turns with 33.0 revolution/minutes
Record player mounted on an inclination of 30∘
(a)
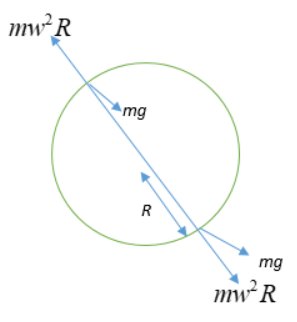
At the topmost point, a gravitational force will act downwards while the centrifugal force will act upward. At the bottom corner of the disc, the centrifugal force and the gravitational force, both act downward. Hence, the net force is very large at this point. So, the bottom most point at the corner is the most critical point for slipping.
(b) No slipping occurs.
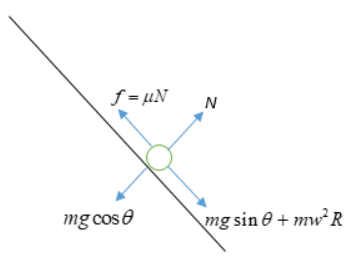
Component of mg in the direction along the plane is mgsinθ
Centrifugal force mw2R in the direction of a Normal force act perpendicular to the disc surface.
Friction forces act in the opposite direction of motion.
So, By balancing equation,
f=μN (1)
N=mgcosθ (2)
f=mgsinθ+mw2R (3)
Substituting values from equation 1 and 2 to 3
μmgcosθ=mgsinθ+mw2R
μmgcosθ=gsinθ+w2R
⇒μ=tanθ+gcosθw2R
⇒As⇒w=33 revol./Min
=2π×6033secrad
=1.1rad/sec.
So, μ=tan30∘+9.8×cos30(1.1)2×0.15
μ=.5773+0.21385
μ=0.5986
Hence, the least possible coefficient of friction is μ=0.5986
Note:
At the lower bottom point where centrifugal force and mg will be minimum behaves as a most Critical point when the angle of inclination is30∘. Also should be aware during calculating of driving force.
