Question
Question: An oil drop of radius 2 mm with a density 3g cm$^{-3}$ is held stationary under a constant electric ...
An oil drop of radius 2 mm with a density 3g cm−3 is held stationary under a constant electric field 3.55 × 105 V m−1 in the Millikan's oil drop experiment. What is the number of excess electrons that the oil drop will possess? (consider g = 9.81 m/s2)
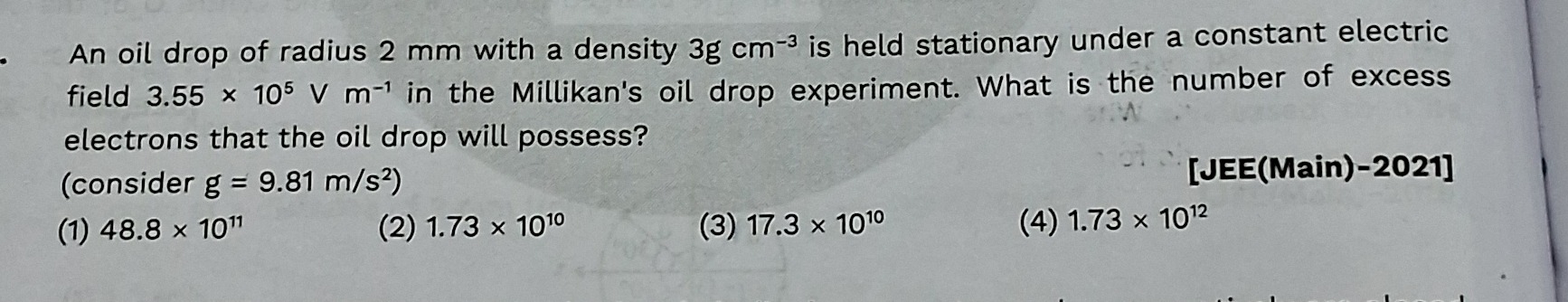
48.8 × 1011
1.73 × 1010
17.3 × 1010
1.73 × 1012
1.73 × 1010
Solution
The oil drop is held stationary under the electric field, which means the net force acting on it is zero. The forces acting on the oil drop are the gravitational force acting downwards and the electric force acting upwards.
The gravitational force is given by Fg=mg, where m is the mass of the oil drop and g is the acceleration due to gravity. The mass of the oil drop can be calculated from its volume and density. Assuming the oil drop is spherical with radius r, its volume is V=34πr3. The mass is m=ρV=ρ34πr3. So, the gravitational force is Fg=ρ34πr3g.
The electric force is given by Fe=∣q∣E, where ∣q∣ is the magnitude of the charge on the oil drop and E is the magnitude of the electric field. If there are n excess electrons, the total charge is q=−ne, where e is the magnitude of the elementary charge (e=1.6×10−19 C). So, the electric force is Fe=neE.
For the oil drop to be stationary, the electric force must balance the gravitational force: Fe=Fg, which means neE=ρ34πr3g.
Solving for n: n=eEρ34πr3g.
Substitute the given values: r=2×10−3 m, ρ=3×103 kg m−3, g=9.81 m/s2, E=3.55×105 V m−1, e=1.6×10−19 C.
n=(1.6×10−19)×(3.55×105)(3×103)×34π(2×10−3)3×9.81≈1.73×1010
